题目内容
【题目】如图,在ABCD中,AB=4,AD=5,tanA=![]() ,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)当点R与点B重合时,求t的值;
(2)当点P在BC边上运动时,求线段PQ的长(用含有t的代数式表示);
(3)当点R落在ABCD的外部时,求S与t的函数关系式;
(4)直接写出点P运动过程中,△PCD是等腰三角形时所有的t值.

【答案】(1)![]() ;(2)
;(2)![]() (9﹣t);(3)①S =﹣
(9﹣t);(3)①S =﹣![]() t2+
t2+![]() t﹣
t﹣![]() ;②S=﹣
;②S=﹣![]() t2+8.③S=
t2+8.③S=![]() (9﹣t)2;(4)4或
(9﹣t)2;(4)4或![]() 或5或
或5或![]() .
.
【解析】
(1)根据题意点R与点B重合时t+![]() t=4,即可求出t的值;
t=4,即可求出t的值;
(2)根据题意运用t表示出PQ即可;
(3)当点R落在□ABCD的外部时可得出t的取值范围,再根据等量关系列出函数关系式;
(4)根据等腰三角形的性质即可得出结论.
解:(1)∵将线段PQ绕点P顺时针旋转90°,得到线段PR,
∴PQ=PR,∠QPR=90°,
∴△QPR为等腰直角三角形.
当运动时间为t秒时,AP=t,PQ=PQ=APtanA=![]() t.
t.
∵点R与点B重合,
∴AP+PR=t+![]() t=AB=4,
t=AB=4,
解得:t=![]() .
.
(2)当点P在BC边上时,4≤t≤9,CP=9﹣t,
∵tanA=![]() ,
,
∴tanC=![]() ,sinC=
,sinC=![]() ,
,
∴PQ=CPsinC=![]() (9﹣t).
(9﹣t).
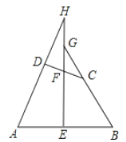
(3)①如图1中,当![]() <t≤3时,重叠部分是四边形PQKB.作KM⊥AR于M.
<t≤3时,重叠部分是四边形PQKB.作KM⊥AR于M.
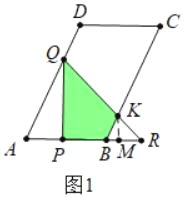
∵△KBR∽△QAR,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴KM=![]() (
(![]() t﹣4)=
t﹣4)=![]() t﹣
t﹣![]() ,
,
∴S=S△PQR﹣S△KBR=![]() ×(
×(![]() t)2﹣
t)2﹣![]() ×(
×(![]() t﹣4)(
t﹣4)(![]() t﹣
t﹣![]() )=﹣
)=﹣![]() t2+
t2+![]() t﹣
t﹣![]() .
.
②如图2中,当3<t≤4时,重叠部分是四边形PQKB.
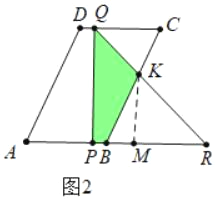
S=S△PQR﹣S△KBR=![]() ×4×4﹣
×4×4﹣![]() ×t×
×t×![]() t=﹣
t=﹣![]() t2+8.
t2+8.
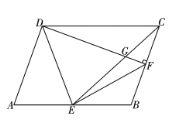
③如图3中,当4<t<9时,重叠部分是△PQK.
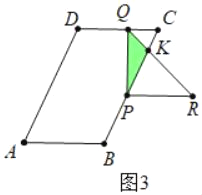
S=![]() S△PQC=
S△PQC=![]() ×
×![]() ×
×![]() (9﹣t)
(9﹣t)![]() (9﹣t)=
(9﹣t)=![]() (9﹣t)2.
(9﹣t)2.
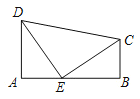
(4)如图4中,
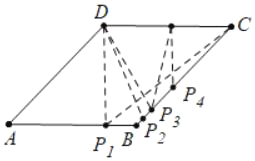
①当DC=DP1=4时,易知AP1=4,t=4.
②当DC=DP2时,CP2=2CD![]() =
=![]() ,
,
∴BP2=![]() ,
,
∴t=4+![]() =
=![]() .
.
③当CD=CP3时,t=5.
④当CP4=DP4时,CP4=2÷![]() =
=![]() ,
,
∴t=9﹣![]() =
=![]() .
.
综上所述,满足条件的t的值为4或![]() 或5或
或5或![]() .
.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案