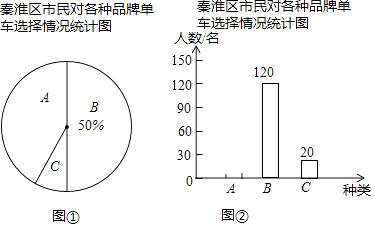
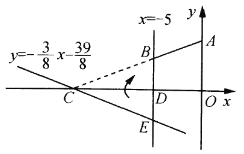
��Ŀ����
����Ŀ���ڡ�ABC�У�DΪBC����һ�㣮
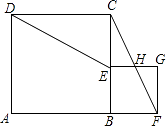
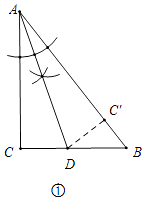
��1����ͼ�٣���Rt��ABC�У���C=90�㣬����ABC����AD�۵�����C����AB���ϣ�����ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
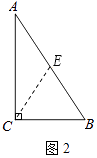
��2����ͼ�ڣ�����ABC���Ź���D��ֱ���۵�����C����AB���ϵ�E����
����DE��AB������ΪE������ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
����AB=4 ![]() ��BC=6����B=45�㣬��CD��ȡֵ��Χ�� ��
��BC=6����B=45�㣬��CD��ȡֵ��Χ�� ��
���𰸡�
��1��
�⣺��D��ͼ��ʾ��������CAB�Ľ�ƽ�����ɣ�
��2���⣺�ٵ�D��ͼ��ʾ��������C��CE��BC����BA���ӳ�����E������CEB�Ľ�ƽ�����ɣ�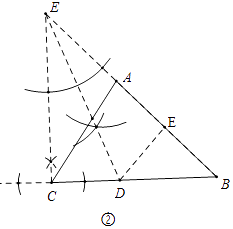
����ͼ���У���CD=DE=x����DE=EB=x����DEB=90�㣬DB= ![]() x��
x��
��BC=6��
��x+ ![]() x=6��
x=6��
��x=6 ![]() ��6��
��6��
��ͼ���У���E��A�غ�ʱ����AH��CB��H����CD=DE=x��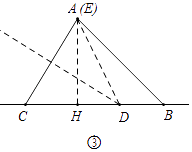
��Rt��AHB�У���֪AH=HB=4����AHB=90�㣬HD=x��2��DE=x��
��x2=42+��x��2��2 ��
��x=5��
���Ͽ�֪��CD�����ֵΪ5����СֵΪ6 ![]() ��6��
��6��
��6 ![]() ��6��CD��5��
��6��CD��5��
�ʴ�Ϊ6 ![]() ��6��CD��5
��6��CD��5
����������1������CAB�Ľ�ƽ�����ɣ���2���ٹ���C��CE��BC����BA���ӳ�����E������CEB�Ľ�ƽ�����ɣ�������ͼ���У����CD����Сֵ������ͼ�۵�E��A�غ�ʱ����AH��CB��H����CD=DE=x�����CD�ɵ�CD�����ֵ��
�����㾫����������Ĺؼ����������ƽ���ߵ����ʶ��������֪ʶ����������1���ڽǵ�ƽ�����ϵĵ㵽����ǵ����ߵľ�����ȣ� ����2��һ���ǵ����ߵľ�����ȵĵ㣬������ǵ�ƽ�����ϣ�