题目内容
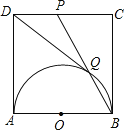
【题目】如图,四边形![]() 是平行四边形,连接对角线
是平行四边形,连接对角线![]() ,过点
,过点![]() 作
作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
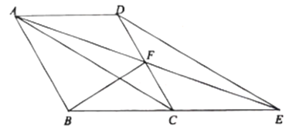
(1)求证:![]() ;
;
(2)连结![]() ,若
,若![]() ,且
,且![]() ,求证:四边形
,求证:四边形![]() 是正方形.
是正方形.
【答案】(1)证明见解析,(2)证明见解析.
【解析】
(1)根据平行四边形的性质得:AD∥BC,AD=BC,又由平行四边形的判定得:四边形ACED是平行四边形,又由平行四边形的对边相等可得结论;
(2)根据(1):四边形ACED是平行四边形,对角线互相平分可得:![]() 结合
结合![]() ,从而证明AD=AB,即邻边相等,证明四边形
,从而证明AD=AB,即邻边相等,证明四边形![]() 为菱形,再证明
为菱形,再证明![]() 从而∠ABC=90°,根据有一个角是直角的菱形是正方形可得结论.
从而∠ABC=90°,根据有一个角是直角的菱形是正方形可得结论.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AC∥DE,
∴四边形ACED是平行四边形,
∴AD=CE,
∴BC=CE;
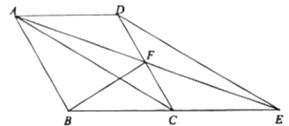
(2)由(1)知:四边形ACED是平行四边形,
∴DF=CF=![]()
![]() AB,EF=AF,
AB,EF=AF,
∵AD=2CF,
∴AB=AD,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() 四边形
四边形![]() 为菱形,
为菱形,
∵AD∥EC,
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴四边形ABCD是正方形.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目