题目内容
已知,开口向上的抛物线y=ax2+bx+c与x轴交于点A(-6,0),另一个交点是B,与y轴的交点是C,且抛物线的顶点的纵坐标是-2,△AOC的面积为6
(1)求点B、C的坐标;
(2)求抛物线的解析式;
(3)M点从点A出发向点C以每秒
个单位匀速运动.同时点P以每秒2个单位的速度从A点出发,沿折线AB、BC向点C匀速运动,在运动的过程中,设△AMP的面积为y,运动的时间为x,求y与x的函数关系式及y的最大值;
(4)在运动的过程中,过点M作MN∥x轴交BC边于N,试问,在x轴上是否存在点Q,使△MNQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
| 3 |
(1)求点B、C的坐标;
(2)求抛物线的解析式;
(3)M点从点A出发向点C以每秒
| ||
| 2 |
(4)在运动的过程中,过点M作MN∥x轴交BC边于N,试问,在x轴上是否存在点Q,使△MNQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)设C(0,c),B(x2,0),
S△AOC=
|c|×6=6
,|c|=2
,
又开口向上,对称轴为x=-2,
∴c<0,
即c=-2
,
-6+x2=-2×2,
x2=2,
点B坐标(2,0),点C坐标(0,-2
);
(2)把点A(-6,0),C(0,-2
)代入y=ax2+bx+c和对称轴-
=-2,得
,
解得
,
∴y=
x2+
x-2
;
(3)如图,
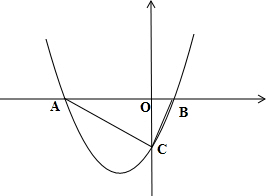
AB=8,AC=4
,BC=4,
△ABC为直角三角形;
如图①,
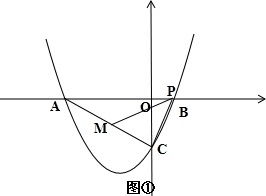
P点运动到点B时,
△AMP的面积最大为y=
×8×
=4
;
当4≤x<6时,沿BC向点C匀速运动,如图②,
AM=
x,PC=12-2x,
△AMP的面积最大为,
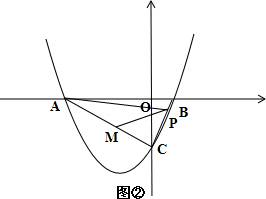
△AMP的面积为y=
AM•PC=
×
x(12-2x),
=-
(x-3)2+
,
这时△AMP的面积最大为
.
综上所知△AMP的面积最大为
;
(4)如图③,
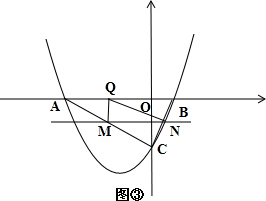
△QMN为直角三角形
∠QMN或∠QNM为直角,
设Q为(x,0),到MN的距离为t,
则QM=-
x-2
=t,点N到x轴的距离是
x-2
=t,
则Q为(-4,0)或(0,0),
当∠MQN为直角时为(0,0);
综上所知Q为(-4,0)或(0,0).
S△AOC=
| 1 |
| 2 |
| 3 |
| 3 |
又开口向上,对称轴为x=-2,
∴c<0,
即c=-2
| 3 |
-6+x2=-2×2,
x2=2,
点B坐标(2,0),点C坐标(0,-2
| 3 |
(2)把点A(-6,0),C(0,-2
| 3 |
| b |
| 2a |
|
解得
|
∴y=
| ||
| 6 |
2
| ||
| 3 |
| 3 |
(3)如图,

AB=8,AC=4
| 3 |
△ABC为直角三角形;
如图①,

P点运动到点B时,
△AMP的面积最大为y=
| 1 |
| 2 |
| 3 |
| 3 |
当4≤x<6时,沿BC向点C匀速运动,如图②,
AM=
| ||
| 2 |
△AMP的面积最大为,

△AMP的面积为y=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=-
| ||
| 2 |
| 9 |
| 2 |
| 3 |
这时△AMP的面积最大为
9
| ||
| 2 |
综上所知△AMP的面积最大为
9
| ||
| 2 |
(4)如图③,

△QMN为直角三角形
∠QMN或∠QNM为直角,
设Q为(x,0),到MN的距离为t,
则QM=-
| ||
| 3 |
| 3 |
| 3 |
| 3 |
则Q为(-4,0)或(0,0),
当∠MQN为直角时为(0,0);
综上所知Q为(-4,0)或(0,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 PE与直线AB交于点E.
PE与直线AB交于点E.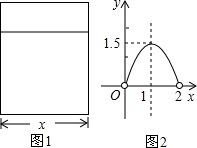 积为ym2,y与x的函数图象如图2所示.
积为ym2,y与x的函数图象如图2所示.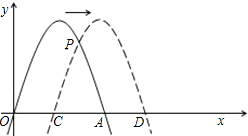 们的长度(可用含m的式子表示);若不存在,请说明理由;
们的长度(可用含m的式子表示);若不存在,请说明理由;