Question

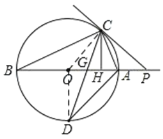
【题目】如图，AB是⊙O的直径，P为BA延长线上一点，过P作⊙O的切线，切点为C，CD平分∠ACB交⊙O于D，交AB于G．

（1）求证：△PAC∽△PCB；

（2）已知⊙O的半径为5，PC＝2，过C作CH⊥AB于H．

①求tan∠ADC；

②求GH的长．

Answer 1

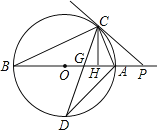
【答案】（1）详见解析；（2）①；②GH＝2﹣．

【解析】

（1）如图，连接OC，先证∠B＝∠ACP，又因为∠CPA＝∠BPC，即可得出结论；

（2）①由（1）知△PAC∽△PCB，利用相似三角形的性质可求出AP的长，可求出∠B的正切值，即可写出∠ADC的正切值；

②如图，连接OD，证OD∥CH，所以△DOG∽△CHG，在Rt△ABC中，设AC＝x，则BC＝x，由勾股定理可求出x的值，即得AC，BC的长，由面积法求出CH的长，由锐角三角函数求出BH的长，进一步求出OH的长，利用相似三角形的性质即可求出GH的长．

（1）证明：如图，连接OC，

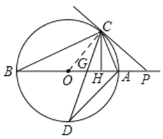
∵PC是⊙O的切线，

∴∠OCP＝90°，

∴∠OCA+∠ACP＝90°，

∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠B+∠CAO＝90°，

∵OC＝OA，

∴∠OCA＝∠OAC，

∴∠B＝∠ACP，

又∵∠CPA＝∠BPC，

∴△PAC∽△PCB；

（2）①由（1）知△PAC∽△PCB，

∴＝＝，

∵PC＝2，AB＝5×2＝10，

∴＝，

∴AP＝2（取正值），

∴＝＝，

∵∠ADC＝∠B，

∴tan∠ADC＝tan∠B＝＝；

②如图，连接OD，

∵CD平分∠ACB，

∴∠BCD＝∠ACD＝ACB＝45°，

∴∠BOD＝∠DOA＝90°，

∵CH⊥AB，

∴∠CHG＝90°＝∠DOA，

∴OD∥CH，

∴△DOG∽△CHG，

在Rt△ABC中，设AC＝x，则BC＝x，

∴x2+（x）2＝102，

∴x＝（取正值），

∴AC＝，BC＝，

∵S△ABC＝BCAC＝ABCH，

∴×＝10CH，

∴CH＝，

∵tan∠B＝，

∴＝＝，

∴BH＝，

∴OH＝BH﹣BO＝﹣5＝，

∵△DOG∽△CHG，

∴＝，

即＝，

∴GH＝2﹣．