题目内容
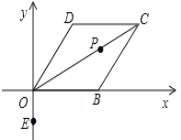
【题目】 菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为( )
A.(2![]() -3,2-
-3,2-![]() )
)
B.(2![]() +3, 2-
+3, 2-![]() )
)
C.(2![]() -3, 2+
-3, 2+![]() )
)
D.(2![]() +3, 2+
+3, 2+![]() )
)
【答案】A
【解析】
试题分析:求一条直线上某一动点到直线同侧两点距离最短的问题,我们一般运用轴对称图形的性质作其中一点关于直线的对称点,转化为一条直线上某一动点到该直线异侧两点距离之和最小,这时根据两点之间线段最短即能确定P点位置,如图,根据菱形的性质,OC、DB互相垂直平分,所以B点关于OC的对称点为D,连接DE,交OC于P'点,P'点即为满足条件的动点P的位置,因为OD=OB=DC=2,∠DOB=60°,求得D(1,![]() ),C(3,
),C(3,![]() ),求P点坐标即是求直线OC与直线DE的交点坐标,根据待定系数法求得直线OC的函数表达式为
),求P点坐标即是求直线OC与直线DE的交点坐标,根据待定系数法求得直线OC的函数表达式为![]() ,同理求得直线DE的函数表达式为
,同理求得直线DE的函数表达式为![]() ,由
,由  解得
解得 ,所以要求的P点坐标为(2
,所以要求的P点坐标为(2![]() -3,2-
-3,2-![]() ).
).
故选A.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目