题目内容
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案.
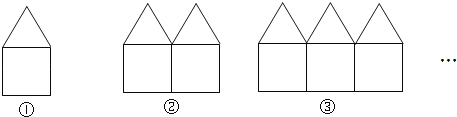
(1)第1个图案中有______根小棒;第2个图案中有__根小棒;第3个图案中有__根小棒;
(2)第n个图案中有多少根小棒?
(3)第25个图案中有多少根小棒?
(4)是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是第几个图案;如果没有,请说明理由.
【答案】(1)6、11、16;(2)(5n+1);(3)126;(4)不存在由2032根小棒摆成的图案.
【解析】
(1)(2)由图可知:第1个图案中有5+1=6根小棒,第2个图案中有2×5+2-1=11根小棒,第3个图案中有3×5+3-2=16根小棒,…由此得出第n个图案中有5n+n-(n-1)=5n+1根小棒;
(3)把数据代入(2)中的规律求得答案即可;
(4)利用(2)中的规律建立方程求得答案即可.
(1)6、11、16;
(2)由图可知:第1个图案中有5+1=6根小棒,第2个图案中有2×5+2﹣1=11根小棒,第3个图案中有3×5+3﹣2=16根小棒,
第n个图案中小棒为5n+n﹣(n﹣1)=5n+1.
所以第n个图案中有(5n+1)根小棒;
(3)当n=25时,5n+1=5×25+1=126,
所以第25个图案中有126根小棒;
(4)因为,5n+1=2032,
所以,n=406.2;
所以不存在由2032根小棒摆成的图案.

练习册系列答案
相关题目