题目内容
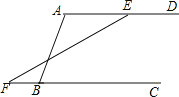
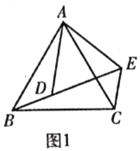
【题目】（1）（问题发现）如图1，
和
均为等边三角形，点
，
，
在同一条直线上.填空：①线段
，
之间的数量关系为______；②
_____°．
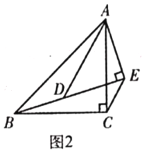
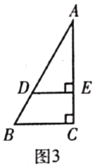
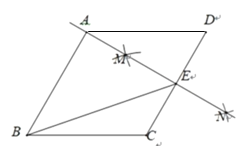
（2）（类比探究）如图2，和均为等腰直角三角形，
，
，
，点，，在同一条直线上，请判断线段，之间的数量关系及
的度数，并给出证明．
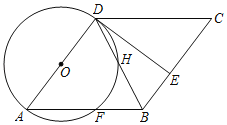
（3）（解决问题）如图3，在中，
，
，
，点在
边上，
于点，
，将绕点
旋转，当
所在直线经过点时，的长是多少？（直接写出答案）
【答案】（1）①
，②60；（2）
，
．证明见解析；（3）
或
．
【解析】
（1）根据等边三角形的性质推出
，即可推出；
，继而推出
；
（2）首先根据
和
均为等腰直角三角形，，可得
，
，进而利用相似三角形的判定和性质解答即可；
（3）分两种情形分别求解即可解决问题．
解：（1）∵和均为等边三角形，
∴
∴
∴
∴；
∵均等边三角形
∴
∴
∵
∴
∴. 
故答案为：①，②60；
（2），.
理由如下：和均为等腰直角三角形，
∴，
，
∴，
，
∵
和
中
，
，
，
∴
，
∴
，
又
∴
，
∴
，
，
∴
，
∵，
∴
，
∴
，
∴；
（3）①如图，当点B在线段ED的延长线上时，连接CD，取AB得中点H，连接EH、CH，
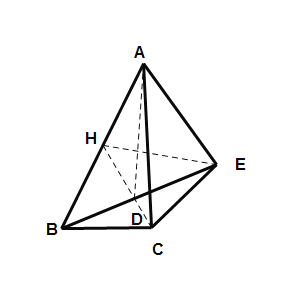
∵，H是AB的中点
∴
∴
∴点A、E、C、B四点在以H为圆心，以
为半径的圆上
∴
∵
∴
∴
∴
∴
∵在
中，
∴
∴
∴
；
②如图，当点B在线段DE的延长线上时，
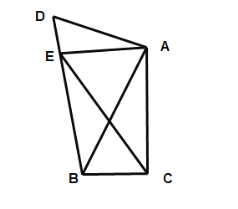
同理可得，
∴
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
