题目内容
【题目】综合与实践:
下面是一个有关平行四边形和等边三角形的小实验,请根据实验解答问题:
已知在□ABCD中,∠ABC=120°,点D又是等边三角形DEF的一个顶点,DE与AB相交于点M,DF与BC相交于点N(不包括线段的端点).
(1)初步尝试:
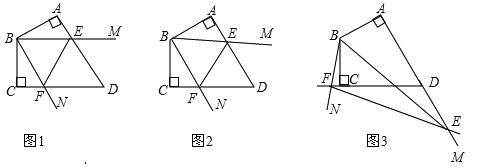
如图①,若AB=BC,求证:BD=BM+BN;
(2)探究发现:
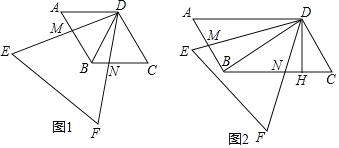
如图②,若BC=2AB,过点D作DH⊥BC于点H,求证:∠BDC=90°.


【答案】(1)(2)见解析.
【解析】试题分析:(1)根据平行四边形的邻角互补得出![]() 又AB=BC,可证△ABD,△BDC都是等边三角形,那么
又AB=BC,可证△ABD,△BDC都是等边三角形,那么![]() 再证明∠ADM=∠BDN.根据ASA证明△ADM≌△BDN,得出AM=BN,进而得出BD=BM+BN;
再证明∠ADM=∠BDN.根据ASA证明△ADM≌△BDN,得出AM=BN,进而得出BD=BM+BN;
(2)直角![]() 中,可求
中,可求![]() 设CH=x,则
设CH=x,则![]()
那么BC=2AB=2DC=4x,BH=BCHC=3x.利用勾股定理求出![]()
那么![]() 根据勾股定理的逆定理得出
根据勾股定理的逆定理得出![]()
试题解析:(1)∵四边形ABCD是平行四边形, ![]() ,
,
![]()
∵AB=BC,
∴AB=BC=CD=DA,
∴△ABD,△BDC都是等边三角形,
![]()
![]()
![]()
∴∠ADM=∠BDN.
在△ADM与△BDN中,
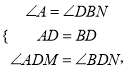
∴△ADM≌△BDN,
∴AM=BN,
∴BD=AB=AM+MB=BN+MB,
即BD=BM+BN;
(2)∵四边形ABCD是平行四边形, ![]()
![]()
∵DH⊥BC, ![]()
![]()
设CH=x,则![]()
∴BC=2AB=2DC=4x,
∴BH=BCHC=3x.
∵DH⊥BC,
![]()
![]()
![]()

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?