题目内容
【题目】如图，A，B两地被大山阻隔，由A地到B地需要绕行C地，若打通穿山隧道，建成A，B两地的直达高铁，可以缩短从A地到B地的路程．已知：∠CAB=30°，∠CBA=45°，AC=580公里，求隧道打通后与打通前相比，从A地到B地的路程将约缩短多少公里？（参考数据：
1.7，
1.4）
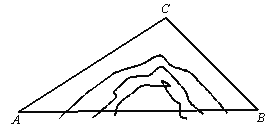
【答案】隧道打通后与打通前相比，从A地到B地的路程将约缩短203公里．
【解析】
过点C作CD⊥AB于点D，利用锐角三角函数的定义求出CD及AD的长，进而可得出结论．
解：过点C作CH⊥AB于H ，
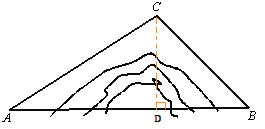
∵在Rt△CHA中，∠A=30°，AC=580，
∴CH＝290，AH＝290
∵ 在Rt△CHB中，∠B=45°，CH＝290，
∴BH＝290，BC＝290
∴AC+BC=580＋290≈986，
AB=AH+BH=290＋290≈783，
∴986－783＝203公里
答：隧道打通后与打通前相比，从A地到B地的路程将约缩短203公里． -
练习册系列答案
相关题目
【题目】抛物线y＝ax2＋bx＋c上部分点的横坐标x和纵坐标y的对应值如下表，则下列说法中正确的有_______．（填序号）
x | … | －4 | －3 | －2 | －1 | 0 | 1 | … |
y | … | －37 | －21 | －9 | －1 | 3 | 3 | … |
①当x＞1时，y随x的增大而减小． ②抛物线的对称轴为直线x＝－
．
③当x＝2时，y＝－9． ④方程ax2＋bx＋c＝0一个正数解
满足1＜＜2．