题目内容
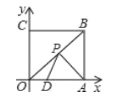
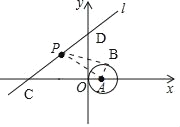
【题目】如图,在平面直角坐标系中,⊙O的圆心A的坐标为(1,0),半径为1,点P为直线y=![]() x+3上的动点,过点P作⊙A的切线,且点为B,则PB的最小值是 .
x+3上的动点,过点P作⊙A的切线,且点为B,则PB的最小值是 .

【答案】2![]()
【解析】分析:因为BP=![]() ,AB的长不变,当PA最小时切线长PB最小,所以点P是过点A向直线l所作垂线的垂足,利用△APC≌△DOC求出AP的长即可求解.
,AB的长不变,当PA最小时切线长PB最小,所以点P是过点A向直线l所作垂线的垂足,利用△APC≌△DOC求出AP的长即可求解.
详解:如图,作AP⊥直线y=![]() x+3,垂足为P,此时切线长PB最小,设直线与x轴,y轴分别交于D,C.
x+3,垂足为P,此时切线长PB最小,设直线与x轴,y轴分别交于D,C.
∵A的坐标为(1,0),∴D(0,3),C(﹣4,0),∴OD=3,AC=5,
∴DC=![]() =5,∴AC=DC,
=5,∴AC=DC,
在△APC与△DOC中,
∠APC=∠COD=90°,∠ACP=∠DCO,AC=DC,
∴△APC≌△DOC,∴AP=OD=3,
∴PB=![]() =2
=2![]() .
.
故答案为2![]() .
.

练习册系列答案
相关题目
【题目】下表给出三种上宽带网的收费方式.
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
![]() 设月上网时间为
设月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() ,直接写出
,直接写出![]() 的解析式,并写出自变量
的解析式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 填空:
填空:![]() 当上网时间 时,选择方式
当上网时间 时,选择方式![]() 最省钱;
最省钱;
![]() 当上网时间 时,选择方式
当上网时间 时,选择方式![]() 最省钱;
最省钱;
![]() 当上网时间 时,选择方式
当上网时间 时,选择方式![]() 最省钱;
最省钱;