题目内容
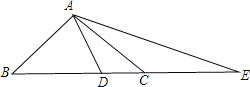
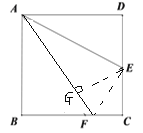
【题目】如图，已知E是正方形ABCD的边CD的中点，点F在BC上，且∠DAE=∠FAE，
求证：AF=AD+CF．
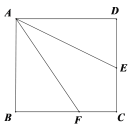
【答案】证明见解析
【解析】
过E点作EG⊥AF，垂足为G，根据题干条件首先证明△ADE≌△AGE，即可得AD＝AG，同理证明出CF＝GF，于是结论可以证明AF＝AD+CF．
过E点作EG⊥AF，垂足为G，
∵∠DAE＝∠FAE，∠D＝∠AGE＝90°，
又∵∠BAE＝∠EAF，即AE为角平分线，EB⊥AB，EG⊥AG，
∴DE＝GE，
在Rt△ADE和Rt△AGE中，
，
∴Rt△ADE≌Rt△AGE（HL），
∴AD＝AG，
∵E是CD的中点，
∴CE=DE=EG，
连接EF，同理可证Rt△ECF≌Rt△EGF，
可得CF＝GF，
∴AF＝AG+GF＝AD＋CF．
练习册系列答案
相关题目
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，有下列说法：
①抛物线与y轴的交点为（0，6）；
②抛物线的对称轴是x=1；
③抛物线与x轴有两个交点，它们之间的距离是 
；
④在对称轴左侧y随x增大而增大．
其中正确的说法是（ ）
A.①②③
B.②③④
C.②③
D.①④
