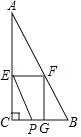Question

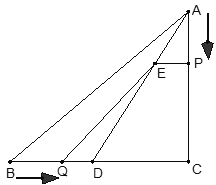
【题目】如图，矩形ABCD为台球桌面，AD=240cm，AB=120cm，球目前在G点位置，AG=80cm，如果小丁瞄准BC边上的点F将球打过去，经过点F反弹后碰到CD边上的点H，再经过点H反弹后，球刚好弹到AD边的中点E处落袋．

（1）求证：△BGF∽△DHE；

（2）求BF的长．

Answer 1

【答案】（1）见详解；（2）90 cm

【解析】

（1）根据两角对应相等的两个三角形相似即可判断．
（2）延长AD交FH的延长线于N，作NM⊥BC交BC的延长线于M．由△GBF∽△NFM，推出 ，由此构建方程即可解决问题．

（1）证明：∵四边形ABCD是矩形，
∴∠B=∠C=∠D=90°，
∵∠GFB=∠HFC，∠FHC=∠EHD，∠HFC+∠FHC=∠DEH+∠EHD=90°，
∴∠HED=∠HFC，
∴∠GFB=∠HED，
∴△BGF∽△DHE；

（2）解：延长AD交FH的延长线于N，作NM⊥BC交BC的延长线于M．

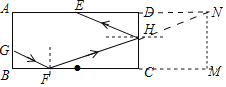
∵∠B=∠M=90°，∠GFB=∠HFC，
∴△GBF∽△NFM，

∴

∴BF=90 cm．