题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .设线段
.设线段![]() 的长为
的长为![]() .
.
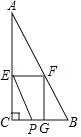
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当四边形![]() 为菱形时,求
为菱形时,求![]() 的值.
的值.
(3)设![]() 与矩形
与矩形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)连结![]() 、
、![]() ,当
,当![]() 与
与![]() 垂直或平行时,直接写出
垂直或平行时,直接写出![]() 的值.
的值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() ;(4)
;(4)![]() 的值是
的值是![]() 或
或![]() .
.
【解析】
(1)先根据平行线分线段成比例定理可得:![]() ,所以表示CE=2x,AE=4-2x,同理得EF的长,证明四边形CEFG为矩形,可得CG=EF=2-x,分P在G的左侧和右侧分别计算PG的长;
,所以表示CE=2x,AE=4-2x,同理得EF的长,证明四边形CEFG为矩形,可得CG=EF=2-x,分P在G的左侧和右侧分别计算PG的长;
(2)先根据两组对边分别平行可得四边形EPBF是平行四边形,当EF=EP时,列方程解出即可;
(3)先计算当P与G重合时,EF=CP,x=1,分两种情况:
①当0<x≤1时,②当1<x<2时,分别根据三角形面积公式可得结论;
(4)当PF⊥EG时,△PFG∽△EGC,列比例式得方程解出即可;
当PF∥EG时,四边形GEFP是平行四边形,根据EF=GP,列方程解出即可.
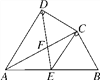
解:(1)如图1,
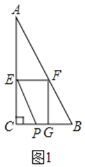
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
或![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
当![]() 时,即
时,即![]() ,
,
![]() ;
;
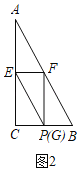
(3)当![]() 与
与![]() 重合时,如图2,
重合时,如图2,![]() ,
,
即![]() ,
,
![]() ,
,
分两种情况:
①当![]() 时,如图1,
时,如图1,![]() ;
;
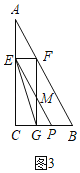
②当![]() 时,如图3,
时,如图3,![]() 交
交![]() 于
于![]() ,
,

∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ;
;
(4)当![]() 时,如图4,
时,如图4,
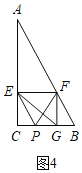
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
当![]() 时,四边形
时,四边形![]() 是平行四边形,
是平行四边形,
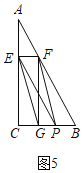
∴![]() ,即
,即![]() ,
,
∴![]() .
.
综上,![]() 的值是
的值是![]() 或
或![]() .
.

练习册系列答案
相关题目