题目内容
【题目】在△ABC中，∠C=90°，AC=4cm，BC=5cm，D在BC上，且CD=3cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以1cm/s的速度，沿AC向终点C移动；点Q以
cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E，连接EQ.设动点运动时间为x秒.
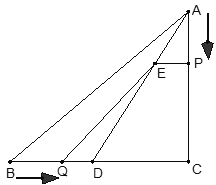
（1）周含x的代表数式表示AE、DE的长度；
（2）当点Q在BD（不包括点B、D）上移动时，设△EDQ的面积为y(cm)，求y与x的函数关系式，并写出自变量x的取值范围；
（3）当x为何值时，△EDQ为直角三角形.
【答案】（1）AE=
，DE=
；（2）
（
）；（3）x=2.5或3.1秒
【解析】
（1）通过△AEP∽△ADC，列出比例关系，即可用含x的代数式表示AE、DE的长度；
（2）Q在BD上运动x秒后，求出DQ、CP，即可表示y与时间x的函数关系式，直接写出自变量x的取值范围；
（3）通过∠EQP=90°，∠QED=90°，分别通过三角形相似，列出比例关系，求出x的值，说明△EDQ为直角三角形．
解：（1）在Rt△ADC中，AC=4，CD=3，
∴AD=5，
∵EP∥DC，
∴△AEP∽△ADC，
,
∴
,
（2）∵BC=5，CD=3，
∴BD=2，
当点Q在BD上运动x秒后，DQ=2-1.25x，
则y= 
即y与x的函数解析式为：，其中自变量的取值范围是：0＜x＜1.6．
（3）分两种情况讨论：
①如图，当∠EQD=90°时，显然有EQ=PC=4-x，
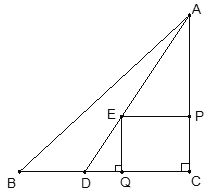
又∵EQ∥AC，
∴△EDQ∽△ADC
又 DQ=1.25x-2
∴
，
解得x=2.5.
②如图，当∠QED=90°时，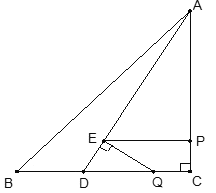
∵∠CDA=∠EDQ，∠QED=∠C=90°
∴△EDQ∽△CDA,
∴
,
∵Rt△EDQ斜边上的高=4-x，
Rt△CDA斜边上的高为=
解得x=3.1．
综上所述，当x为2.5秒或3.1秒时，△EDQ为直角三角形．
