题目内容
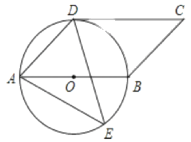
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE+FH的最大值为( )

A.8B.12C.16D.20
【答案】B
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为8,可得AB=OA=OB=8,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
如图所示,连接OA、OB,

∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵O的半径为8,
∴AB=OA=OB=8,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=4,
AB=4,
∵GE+EF+FH=GH,EF为定值,
∴当GH最大时,GE+FH最大
∵当弦GH是圆的直径时,它的最大值为:8×2=16,
∴GE+FH的最大值为:164=12.
故选B.

练习册系列答案
相关题目
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)求售价为多少元时每天获得利润最大,最大利润是多少?