题目内容
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
(1)求A、B两点的坐标。
(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.
(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.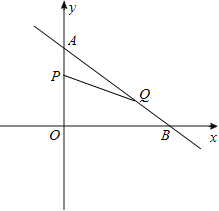
【答案】(1)A(0,3), B(4,0)(2)t=![]() ,Q(
,Q(![]() );t=
);t=![]() ,Q(
,Q(![]() )(3)存在。M1(
)(3)存在。M1(![]() ), M2(
), M2(![]() ),M3(
),M3(![]() )
)
【解析】
解:(1)由x2-7 x +12=0解得x1=3,x2=4。
∵OA<OB ,∴OA="3" , OB=4。∴A(0,3), B(4,0)。
(2)由OA="3" , OB=4,根据勾股定理,得AB=5。
由题意得,AP=t, AQ=5-2t 。分两种情况讨论:
①当∠APQ=∠AOB时,如图1,
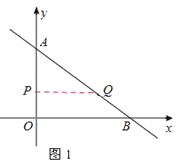
△APQ∽△AOB。∴![]() ,即
,即![]() 解得 t=
解得 t=![]() 。∴Q(
。∴Q(![]() )。
)。
②当∠AQP=∠AOB时,如图2,
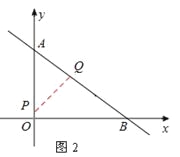
△APQ∽△ABO。∴![]() ,即
,即![]() 解得 t=
解得 t=![]() 。∴Q(
。∴Q(![]() )。
)。
(3)存在。M1(![]() ), M2(
), M2(![]() ),M3(
),M3(![]() )。
)。
(1)解出一元二次方程,结合OA<OB即可求出A、B两点的坐标。
(2)分∠APQ=∠AOB和∠AQP=∠AOB两种情况讨论即可。
(3)当t=2时,如图,
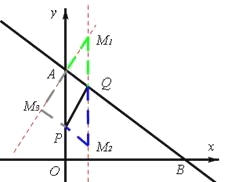
OP=2,BQ=4,∴P(01),Q(![]() )。
)。
若以A、P、Q、M为顶点的四边形是平行四边形,则
①当AQ为对角线时,点M1的横坐标与点Q的横坐标相同,纵坐标为![]() 。∴M1(
。∴M1(![]() )。
)。
②当PQ为对角线时,点M2的横坐标与点Q的横坐标相同,纵坐标为![]() 。∴M2(
。∴M2(![]() )。
)。
③当AP为对角线时,点Q、M3关于AP的中点对称。
由A(0,3),P(0,1)得AP的中点坐标为(0,2)。
由Q(![]() )得M3的横坐标为
)得M3的横坐标为![]() ,纵坐标为
,纵坐标为![]() 。∴M3(
。∴M3(![]() )。
)。
综上所述,若以A、P、Q、M为顶点的四边形是平行四边形,则M点的坐标为
(![]() )或(
)或(![]() )或(
)或(![]() )。
)。



