题目内容
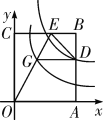
【题目】矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=![]() 与边AB交于点D,过点D作DG∥OA,交双曲线y=
与边AB交于点D,过点D作DG∥OA,交双曲线y=![]() (k>0)于点G,连接OG并延长交CB于点E,若∠EGD=∠EDG,则k的值为______.
(k>0)于点G,连接OG并延长交CB于点E,若∠EGD=∠EDG,则k的值为______.
【答案】![]()
【解析】
先根据OA=4,OC=6,点D在双曲线y=![]() 上求出D点的坐标,再由DG∥OA得出G点纵坐标,设出G、E两点坐标,根据∠EGD=∠EDG即可得出EG=ED,再根据GE两点共线可得出G点坐标,代入双曲线y=
上求出D点的坐标,再由DG∥OA得出G点纵坐标,设出G、E两点坐标,根据∠EGD=∠EDG即可得出EG=ED,再根据GE两点共线可得出G点坐标,代入双曲线y=![]() (k>0)即可得出k的值.
(k>0)即可得出k的值.
解:∵在矩形OABC中,OA=4,
∴直线AB的解析式为x=4,
∵点D在双曲线y=![]() 上,
上,
∴D(4,2).
∵DG∥OA,
∴设G(a,2),E(b,6).
∵∠EGD=∠EDG,
∴点E在线段GD的垂直平分线上,
∴![]() =b①.设直线OG的解析式为y=cx(c≠0).
=b①.设直线OG的解析式为y=cx(c≠0).
∵点G,E均在直线上,
∴2=ca,6=cb,
∴![]() =
=![]() ②,联立①②,解得a=
②,联立①②,解得a=![]() ,
,
∴G(![]() ,2).
,2).
∵点G在双曲线y=![]() 上,
上,
∴k=![]() ×2=
×2=![]() .
.

练习册系列答案
相关题目