题目内容
【题目】某工厂拟建一个如图所示的矩形仓库ABCD,仓库的一边是长为12m的一面墙,另外三边用30m长的建筑材料围成.设AB的长为xm,矩形ABCI的面积为Sm2.
(1)用含x的代数式表示BC的长,并求出x的取值范围.
(2)写出S关于x的函数关系式,并求出S的最大值.

【答案】(1)9≤x<15(2)当x=9时,S最大=108cm2
【解析】
(1)根据题意列不等式即可得到结论;
(2)根据题意得到函数关系式,根据二次函数的性质即可得到结论;
解:(1)根据题意得:BC=(30-2x)m
![]()
解得:9≤x<15,
∴x的取值范围为:9≤x<15;
(2)根据题意得,S=x(30-2x)=-2x2+30x 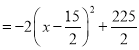
∵9≤x<15且a=-2<0,
∴当x=9时,S最大=108m2;

练习册系列答案
相关题目