��Ŀ����
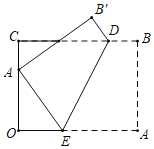
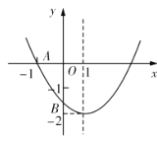
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y��x+4��y��kx+4�ֱ�x���ڵ�A��B����ֱ�߽���y����ͬһ��C����D������Ϊ(��![]() ��0)����E��AC���е㣬����OE��CD�ڵ�F��
��0)����E��AC���е㣬����OE��CD�ڵ�F��
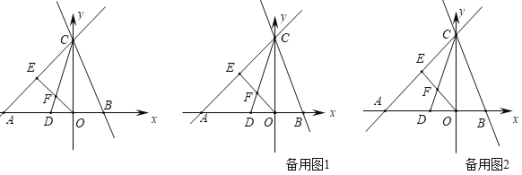
��1�����F�����ꣻ
��2������OCB����ACD����k��ֵ��
��3���ڣ�2���������£�����F��x��Ĵ���1����M��ֱ��BC�ϵĶ��㣬��N��x���ϵĶ��㣬��P��ֱ��l�ϵĶ��㣬ʹ����B��P��M��NΪ������ı��������Σ����P�����꣮
���𰸡���1��F(��1��1)����2����2����3��P������Ϊ(��1��![]() )��(��1��
)��(��1��![]() )��(��1����6)
)��(��1����6)
��������
��1�����ֱ��OE��ֱ��CD�Ľ���ʽ�����������鼴�ɽ�����⣮
��2����ͼ2�У����߶�DC�Ƶ�D˳ʱ����ת90���õ�DT����ֱ��CT��x����B��֤����ACO����DCB��45���������Ƴ���ACD����OCB�������T�����꣬���ô���ϵ�������ɽ�����⣮
��3����ͼ3�У����������Σ����ı���BN1P1M1������ʱ�����ı���BN2P2M2������ʱ�����ı���BP3N3M3������ʱ���ֱ���⼴�ɽ�����⣮
�⣺��1����ͼ1�У�
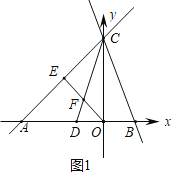
��ֱ��y��x+4��x����A����y����C��
��A����4��0����C��0��4����
��AE��EC��
��E����2��2����
��ֱ��OE�Ľ���ʽΪy����x��
��![]()
��ֱ��CD�Ľ���ʽΪy��3x+4��
��![]() �����
�����![]()
��F����1��1����
��2����ͼ2�У����߶�DC�Ƶ�D˳ʱ����ת90���õ�DT����ֱ��CT��x����B��
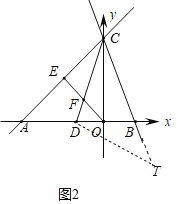
��DC��DT����CDT��90����
���DCT��45����
��OA��OC����AOC��90����
���ACO����DCT��45����
���ACD����OCB��
��![]()
��![]() ����y��kx+4���õ�k����2��
����y��kx+4���õ�k����2��
��3����ͼ3�У�
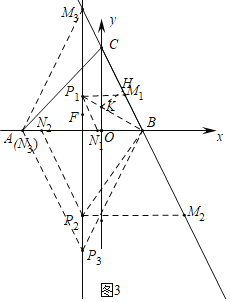
���ı���BN1P1M1������ʱ������BP1��OC��K����KH��BC��H��
�ߡ�KBO����KBH��KO��OB��KH��BC��
��KO��KH��
��BK��BK����KOB����KHB��90����
��Rt��KBO��Rt��KBH��HL����
��BO��BH��2����OK��KH��x��
��![]()
��![]()
��Rt��CHK��CK2��KH2+CH2��
��![]()
��![]()
��ֱ��BK�Ľ���ʽΪ![]()
��x����1ʱ��![]()
��
���ı���BN2P2M2������ʱ���ɵ�ֱ��BP2�Ľ���ʽΪ![]()
��x����1ʱ��![]()
��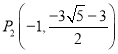
���ı���BP3N3M3������ʱ��M3��ֱ��x����1ʱ
��M3����1��6����
��P3��M3����x��Գƣ�
��P3����1����6����
�������������������ĵ�P������Ϊ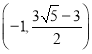 ��
��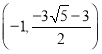 ��1����6����
��1����6����

 �ŵ������ϵ�д�
�ŵ������ϵ�д�����Ŀ��ijУΪ�˽��ߡ����꼶ѧ��Ӣ������ѵ��������ߡ����꼶ѧ��������ͬ����ij�ܴ��������꼶ѧ���зֱ���������30��ͬѧ��������������һ�����������ѵ����������ݵ�������õ�����ͳ��ͼ����
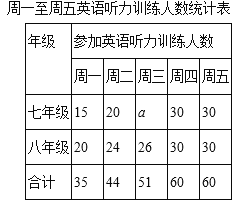

��1����գ�a���� ����
��2����������ͳ��ͼ������±��е����ͳ������
�꼶 | ƽ��ѵ��ʱ�����λ�� | �μ�Ӣ������ѵ�������ķ��� |
���꼶 | 24 | 34 |
���꼶 | �� �� | 14.4 |
��3��������������ͳ��ͼ�����ߡ����꼶Ӣ������ѵ�����д���������������ۣ�
��4����������һ������Ӣ������ѵ������ͳ�Ʊ������Ƹ�У�ߡ����꼶��480��ѧ������һ������ƽ��ÿ���ж����˽���Ӣ������ѵ����