题目内容
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() .
.
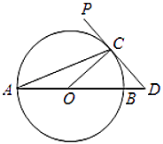
(1)求![]() 的度数.
的度数.
(2)若![]() 的半径为2,求
的半径为2,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据等腰三角形性质和三角形外角性质求出∠COD=2∠A,求出∠D=∠COD,根据切线性质求出∠OCD=90°,即可求出答案;
(2)由题意![]() 的半径为2,求出OC=CD=2,根据勾股定理求出BD即可.
的半径为2,求出OC=CD=2,根据勾股定理求出BD即可.
解:(1)∵OA=OC,
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵∠D=2∠A,
∴∠D=∠COD,
∵PD切⊙O于C,
∴∠OCD=90°,
∴∠D=∠COD=45°;
(2)∵∠D=∠COD,![]() 的半径为2,
的半径为2,
∴OC=OB=CD=2,
在Rt△OCD中,由勾股定理得:22+22=(2+BD)2,
解得:![]() .
.

练习册系列答案
相关题目
【题目】小敏打算在某外卖网站点如下表所示的菜品和米饭.已知每份订单的配送费为3元,商家为促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元.如果小敏在购买下表的所有菜品和米饭时,采取适当的下单方式,那么他的总费用最低可为( )
菜品 | 单价(含包装费) | 数量 | |
| 水煮牛肉(小) | 30元 | 1 |
| 醋溜土豆丝(小) | 12元 | 1 |
| 豉汁排骨(小) | 30元 | 1 |
| 手撕包菜(小) | 12元 | 1 |
| 米饭 | 3元 | 2 |
A.48元B.51元C.54元D.59元