题目内容
【题目】综合题。
（1）问题发现：
如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为
（2）拓展探究：
在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE、CE、AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）问题解决：
当正方形CDEF旋转到B、E、F三点共线时候，直接写出线段AF的长．
【答案】
（1）BE= 
AF；
（2）
解：无变化；理由如下：
如图2，在Rt△ABC中，AB=AC=2，
∴∠ABC=∠ACB=45°，
∴sin∠ABC= 
，
在正方形CDEF中，∠FEC= 
∠FED=45°，
在Rt△CEF中，sin∠FEC= 
= 
，
∴ 
，
∵∠FCE=∠ACB=45°，
∴∠FCE﹣∠ACE=∠ACB﹣∠ACE，
∴∠FCA=∠ECB，
∴△ACF∽△BCE，
∴ 
= ，
∴BE= AF，
∴线段BE与AF的数量关系无变化；
（3）
解：当点E在线段AF上时，如图2，
由（1）知，CF=EF=CD= ，
在Rt△BCF中，CF= ，BC=2 ，
根据勾股定理得，BF= 
，
∴BE=BF﹣EF= ﹣ ，
由（2）知，BE= AF，
∴AF= 
﹣1，
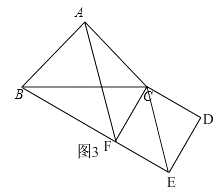
当点E在线段BF的延长线上时，如图3，
在Rt△ABC中，AB=AC=2，
∴∠ABC=∠ACB=45°，
∴sin∠ABC═ ，
在正方形CDEF中，∠FEC= ∠FED=45°，
在Rt△CEF中，sin∠FEC= = ， ，
∵∠FCE=∠ACB=45°，
∴∠FCB+∠ACB=∠FCB+∠FCE，
∴∠FCA=∠ECB，
∴△ACF∽△BCE，
∴ 
= 
= ，
∴BE= AF，
由（1）知，CF=EF=CD= ，
在Rt△BCF中，CF= ，BC=2 ，
根据勾股定理得，BF= ，
∴BE=BF+EF= + ，
由（2）知，BE= AF，
∴AF= +1．
即当正方形CDEF旋转到B、E、F三点共线时候，线段AF的长为 ﹣1或 +1
【解析】解：（1）在Rt△ABC中，AB=AC=2，
根据勾股定理得，BC= AB=2 ，
点D为BC的中点，
∴AD= BC= ，
∵四边形CDEF是正方形，
∴AF=EF=AD= ，
∵BE=AB=2，
∴BE= AF，
所以答案是：BE= AF；
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
