题目内容
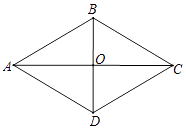
【题目】四边形ABCD是菱形，∠BAD=60°，AB=6，对角线AC与BD相交于点O，点E在AC上，若OE= 
，则CE的长为 ．
【答案】4 
或2
【解析】解：∵四边形ABCD是菱形， ∴AB=AD=6，AC⊥BD，OB=OD，OA=OC，
∵∠BAD=60°，
∴△ABD是等边三角形，
∴BD=AB=6，
∴OB= 
BD=3，
∴OC=OA= 
=3 ，
∴AC=2OA=6 ，
∵点E在AC上，OE= ，
∴CE=OC+ 或CE=OC﹣ ，
∴CE=4 或CE=2 ；
故答案为：4 或2 ．
由菱形的性质证出△ABD是等边三角形，得出BD=AB=6，OB= BD=3，由勾股定理得出OC=OA= =3 ，即可得出答案．
练习册系列答案
相关题目
