题目内容
【题目】综合题 1、如图1，线段AB的端点在正方形网格的格点上，在图1中找到格点C，使组成的△ABC的一个内角α满足tanα=2（找到两个点C，全等的三角形算一种）
2、
（1）如图1，线段AB的端点在正方形网格的格点上，在图1中找到格点C，使组成的△ABC的一个内角α满足tanα=2（找到两个点C，全等的三角形算一种）．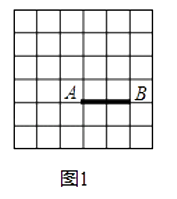
（2）如图2，在Rt△DEF中，∠DEF=90°，DE=1，sin∠F= 
．用两块全等的△DEF拼出一个平行四边形，将拼得的平行四边形画在图2网格（网格图中小正方形边长均为1）中，画出不同的两种平行四边形（全等的算一种），并写出相应的周长．
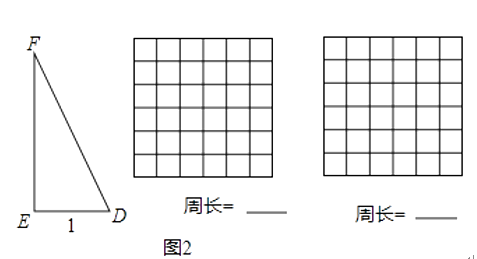
【答案】
（1）解：如图△ABC，△ABC′即为所求；
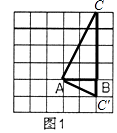
（2）解：有三种拼法：周长分别为8，2+2 
，6+2 ．
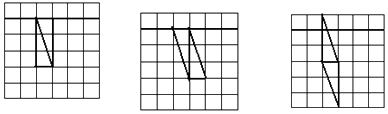
【解析】（1）根据已知tanα=2，因此画出的直角三角形的两直角边存在2倍关系即可。
（2）先利用解直角三角形算出EF、DE的长，有三种拼法：分别以DE、DF、EF为所拼的平行四边形的对角线，再分别求出周长即可。
【考点精析】本题主要考查了平行四边形的性质和解直角三角形的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．
练习册系列答案
相关题目
