题目内容
【题目】已知抛物线C1：y=﹣ 
x2+bx+c的对称轴是x=2，且经过点（6，0）．
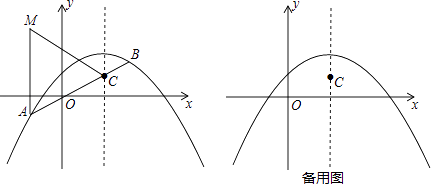
（1）求抛物线C1的解析式；
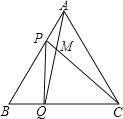
（2）将抛物线C1向下平移2个单位后得到抛物线C2 ， 如图，直线y=kx﹣2k+1交抛物线C2于A，B两点（点A在点B的左边），交抛物线C2的对称轴于点C，M（xA ， 3），xA表示点A横坐标，求证：AC=AM；
（3）在（2）的条件下，请你参考（2）中的结论解决下列问题：
①若CM=AM，求 
的值；
②请你探究：在抛物线C2上是否存在点P，使得PO+PC取得最小值？如果存在，求出点P的坐标；如果不存在，请说明理由．
【答案】
（1）解：∵抛物线C1的对称轴为直线x=2，且抛物线与x轴的一个交点坐标为（6，0），
∴抛物线与x轴的另一个交点坐标为（﹣2，0），
∴抛物线C1的解析式为y=﹣ 
（x+2）（x﹣6），
即y=﹣ x2+x+3
（2）证明：∵抛物线C1的解析式为y=﹣ （x﹣2）2+4，
∴抛物线C2的解析式为y=﹣ （x﹣2）2+2，
∵直线y=kx﹣2k+1过定点（2，1），
而直线y=kx﹣2k+1交抛物线C2的对称轴于点C，
∴C（2，1），
设A[x，﹣ （x﹣2）2+2）]，
∴AC2=（x﹣2）2+[﹣ （x﹣2）2+2﹣1]2= 
（x﹣2）4+ 
（x﹣2）2+1，
AM2=[﹣ （x﹣2）2+2﹣3]2= （x﹣2）4+ （x﹣2）2+1，
∴AC=AM
（3）解：①∵AC=AM，CM=AM，
∴△ACM是等边三角形．
∴∠AMC=∠ACM=60°，
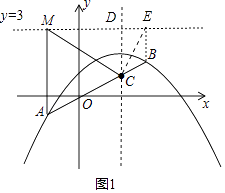
直线y=3交直线x=2于D点，过点B作BE⊥直线y=3于点E，如图1，则由（2）可知BC=BE，易证∠MCD=60°，∠BCE=∠DCE=30°，
在Rt△CDE中，tan∠DCE=tan30°= 
= 
，
在Rt△CDM中，tan∠CMD=tan30°= 
= ，
∴ 
= 
，
∵AM∥DC∥EB，
∴ 
= = ；
②存在．
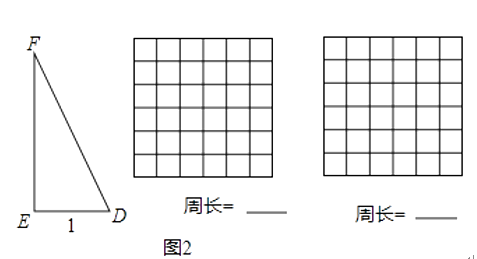
如图2，y轴与抛物线的交点记作点P，与直线y=3的交点记作点H，
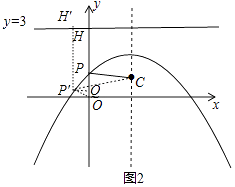
由（2）可知PC=PH，
如图，在抛物线上取异于点P的P′，作P′H′⊥直线y=3于H′，P′Q⊥y轴于点Q，
由（2）可知P′C=PH′，
易得四边形HH′P′Q为矩形，
∴P′H′=QH，
∵OP′＞OQ，
∴OQ+QH＜OP′+P′H′，
∴OP+PH＜OP′+P′C，
∴点P（0，1）使得PO+PC取得最小值．
【解析】（1）根据已知点的坐标和对称轴求出此抛物线与x轴的另一个交点坐标，即可求出抛物线的解析式。
（2）先抛物线C1写成顶点式，再根据平移规律（上加下减），求出抛物线C2的函数解析式，而交抛物线C2的对称轴于点C，，可知点C（2，1），再设出点A的坐标，利用勾股定理求出AC2、AM2即可得到AC=AM。
（3）①由已知易征得△ACM是等边三角形．直线y=3交直线x=2于D点，过点B作BE⊥直线y=3于点E，在Rt△CDE中和Rt△CDM中，利用解直角三角形得出 、的值，从而得到DE:DM的值，再由AM∥DC∥EB，得出对应线段成比例，即可求得结果；②y轴与抛物线的交点记作点P，与直线y=3的交点记作点H，先证明四边形HH′P′Q为矩形，得到P′H′=QH，再利用OP′＞OQ得出OP+PH＜OP′+P′C，，于是可判断点P（0，1）使得PO+PC取得最小值。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
