题目内容
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;
②当x= ![]() 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确结论是 . (填序号)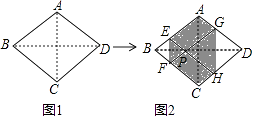
【答案】①④
【解析】解:∵菱形ABCD的边长为2,
∴AB=BC=2,
∵∠ABC=60°,
∴AC=AB=2,BD=2 ![]() ,
,
由折叠知,△BEF是等边三角形,
当x=1时,则AE=1,
∴BE=AB﹣AE=1,
由折叠知,BP=2× ![]() =
= ![]() =
= ![]() BD,
BD,
∴点P是菱形ABCD的对角线的交点,
即:点P是菱形ABCD的中心,所以①正确,
如图,
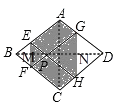
∵AE=x,
∴BE=AB﹣AE=2﹣x,
∵△BEF是等边三角形,
∴EF=BE=2﹣x,
∴BM= ![]() EM=
EM= ![]() ×
× ![]() EF=
EF= ![]() (2﹣x),
(2﹣x),
∴BP=2BM= ![]() (2﹣x),
(2﹣x),
∴DP=BD﹣BP=2 ![]() ﹣
﹣ ![]() (2﹣x)=
(2﹣x)= ![]() x,
x,
∴DN= ![]() DP=
DP= ![]() x,
x,
∴GH=2GN=2× ![]() x=x,
x=x,
当x= ![]() 时,AE=
时,AE= ![]() ,
,
∴BE=AB﹣AE= ![]() ,
,
∵△BEF是等边三角形,
∴EF=BE= ![]() ,BP=
,BP= ![]() ,
,
∴DP= ![]() ,
,
∴GH=DG= ![]() ,
,
∴EF+GH=2=AC,所以②错误;
当0<x<2时,
∵AE=x,
∴BE=2﹣x,
∴EF=2﹣x,
∴BP= ![]() (2﹣x),
(2﹣x),
∴DP= ![]() x,
x,
∴GH=2× ![]() =x=DG=DH,
=x=DG=DH,
∴六边形AEFCHG面积=S菱形ABCD﹣S△BEEF﹣S△DGH
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() (2﹣x)2﹣
(2﹣x)2﹣ ![]() x2
x2
=2 ![]() ﹣
﹣ ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]()
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1时,六边形AEFCHG面积最大为 ![]() ,所以③错误,
,所以③错误,
六边形AEFCHG周长=AE+EF+FC+CH+HG+AG
=x+2﹣x+x+2﹣x+x+2﹣x=6是定值,
所以④正确,即:正确的有①④,
所以答案是①④.
【考点精析】关于本题考查的二次函数的最值和菱形的性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.