题目内容
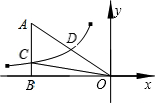
如图，已知双曲线y=
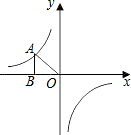
(k＜0)经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（-6，4），则△AOC的面积为______．
| k |
| x |
∵点D为△OAB斜边OA的中点，且点A的坐标（-6，4），
∴点D的坐标为（-3，2），
把（-3，2）代入双曲线y=
(k＜0)，
可得k=-6，
即双曲线解析式为y=-
，
∵AB⊥OB，且点A的坐标（-6，4），
∴C点的横坐标为-6，代入解析式y=-
，
y=1，
即点C坐标为（-6，1），
∴AC=3，
又∵OB=6，
∴S△AOC=
×AC×OB=9．
故答案为：9．
∴点D的坐标为（-3，2），
把（-3，2）代入双曲线y=
| k |
| x |
可得k=-6，
即双曲线解析式为y=-
| 6 |
| x |
∵AB⊥OB，且点A的坐标（-6，4），
∴C点的横坐标为-6，代入解析式y=-
| 6 |
| x |
y=1，
即点C坐标为（-6，1），
∴AC=3，
又∵OB=6，
∴S△AOC=
| 1 |
| 2 |
故答案为：9．
练习册系列答案
全能测控期末小状元系列答案
相关题目
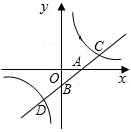A点的坐标为（2，0），点C、D分别在第一、第三象限，且OA=OB=AC=BD，试求：
