题目内容
【题目】定义:如果一个四边形的两条对角线相等且相互垂直,则称这个四边形为“等垂四边形”.
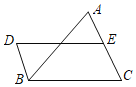
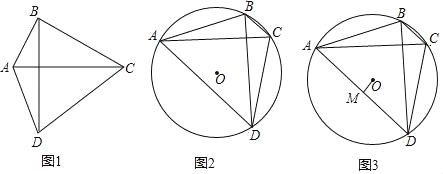
如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为“等垂四边形.根据等垂四边形对角线互相垂直的特征可得等垂四边形的一个重要性质:等垂四边形的面积等于两条对角线乘积的一半.根据以上信息解答下列问题:
(1)矩形 “等垂四边形”(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是等垂四边形,若⊙O的半径为6,∠ADC=60°,求四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是等垂四边形,作OM⊥AD于M.请猜想OM与BC的数量关系,并证明你的结论.
【答案】(1)不是;(2)54;(3)OM=![]() BC.
BC.
【解析】
(1)矩形的对角线相等,不一定垂直,所以矩形不一定是等垂四边形.
(2)连接OA,OC,过O作OH⊥AC于H,利用垂径定理求出AC的长即可解决问题;
(3)连接OA,OB,OC,OD,过O作OE⊥BC于E,只要证明△OAM≌△BOE即可解决问题.
解:(1)矩形的对角线相等,不一定垂直,所以矩形不一定是等垂四边形.
故答案为:不是;
(2)连接OA,OC,过O作OH⊥AC于H.
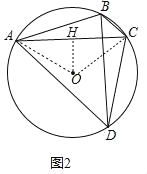
在△AOH中,∠AOH=∠ADC=60,OA=6,
∴AH=3![]() ,
,
∴AC=2AH=6![]() ,
,
∵四边形ABCD是等垂四边形,
∴AC=BD=6![]()
∴S四边形ABCD=![]() ACBD=
ACBD=![]() ×6
×6![]() ×6
×6![]() =54.
=54.
(3)连接OA,OB,OC,OD,过O作OE⊥BC于E,
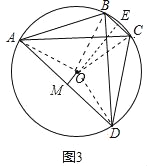
显然∠BOE=∠BAC,∠AOM=∠ABD,
∵BD⊥AC,
∴∠ABD﹢∠BAC=90,
∵∠AOM﹢∠OAM=90,
∴∠OAM=∠BOE,
在△OAM中与△BOE中,
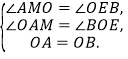
∴△OAM≌△BOE,
∴OM=BE,
∵BE=![]() BC,
BC,
∴OM=![]() BC.
BC.
故答案为:(1)不是;(2)54;(3)OM=![]() BC.
BC.

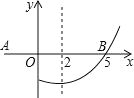
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大