题目内容
【题目】如图是二次函数![]() 的图象的一部分,对称轴是直线
的图象的一部分,对称轴是直线![]() .
.
①![]() ; ②
; ②![]() ; ③不等式
; ③不等式![]() 的解集是
的解集是![]() ;④若
;④若![]() ,
,![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() . 上述
. 上述![]() 个判断中,正确的是( )
个判断中,正确的是( )
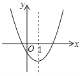
A. ①④ B. ①②④ C. ①③④ D. ②③④
【答案】A
【解析】
根据抛物线与x轴的交点个数对①进行判断;由于不能确定抛物线与x轴的交点坐标,于是可对②③进行判断;当抛物线开口向上,抛物线上的点到对称轴的距离越远,对应的函数值越大,由此可对④进行判断.
解:∵抛物线与x轴有2个交点,
∴b2-4ac>0,即b2>4ac,所以①正确;
∵抛物线的对称轴是直线x=1,但不能确定抛物线与x轴的交点坐标,
∴4a+2b+c<0不确定;不等式ax2+bx+c>0的解集x≥3.5错误,所以②③错误;
∵点(-2,y1)比点(5,y2)到直线x=1的距离小,
而抛物线开口向上,
∴y1<y2,所以④正确.
故①④正确.
故选A

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.