题目内容
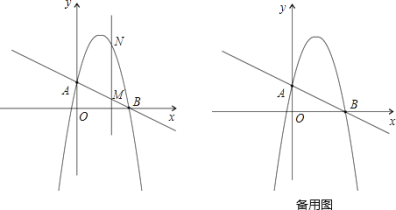
【题目】平面直角坐标系中,点O是坐标原点,抛物线y=ax2+![]() x+c与x轴交于A、B两点,点B的坐标为(4,0),与y轴交于点C,直线y=kx+2经过A、C两点.
x+c与x轴交于A、B两点,点B的坐标为(4,0),与y轴交于点C,直线y=kx+2经过A、C两点.
(1)如图1,求a、c的值;
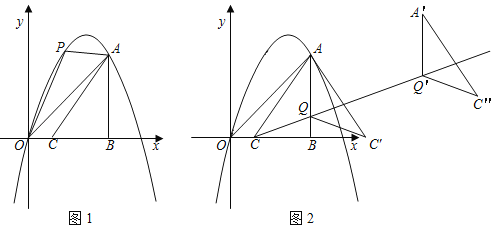
(2)如图2,点P为抛物线y=ax2+![]() x+c在第一象限的图象上一点,连接AP、CP,设点P的橫坐标为t,△ACP的面积为S,求S与t的函数解析式,并直接写出自变量t的取值范围;
x+c在第一象限的图象上一点,连接AP、CP,设点P的橫坐标为t,△ACP的面积为S,求S与t的函数解析式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,点D为线段AC上一点,直线OD与直线BC交于点E,点F是直线OD上一点,连接BP、BF、PF、PD,BF=BP,∠FBP=90°,若OE=![]() ,求直线PD的解析式.
,求直线PD的解析式.
【答案】(1)a=![]() 、c=2;(2)S=
、c=2;(2)S=![]() t2+
t2+![]() t(0<t<4);(3)直线PD的解析式为y=
t(0<t<4);(3)直线PD的解析式为y=![]() x+
x+![]() .
.
【解析】
(1)令y=kx+2中x=0,可得出点C的坐标,再将B,C的坐标代入y=ax2+![]() x+c,可求出a,c的值;
x+c,可求出a,c的值;
(2)过点P作x轴的垂线,垂足为点M,且与直线AC交于点K,过点C作PK的垂线,垂足为点N,先求出点A的坐标,从而可得出直线y=kx+2的解析式,由P点的横坐标为t,可得P(t,﹣![]() t2+
t2+![]() t+2),K(t,2t+2),得出PK=
t+2),K(t,2t+2),得出PK=![]() t2+
t2+![]() t,最后根据S=S△AMK﹣S△AMP﹣S△CPK可得出函数解析式;
t,最后根据S=S△AMK﹣S△AMP﹣S△CPK可得出函数解析式;
(3)过点O作OH⊥BC于点H,结合面积法和勾股定理可先求出OH,BH的长,进一步可得出EH,BE,CE的长;过点E作EG⊥y轴于点G,先得出tan∠CEG=tan∠OBE=![]() ,可求出CG,EG的长,从而可求出点E的坐标,利用待定系数法可求出直线OE的解析式,再与直线AC的解析式联立可求出点D坐标;过点B作x轴的垂线,与过点P、F作的y轴的垂线分别交于Q、T两点,先证明△PQB≌△BTF,从而有BT=PQ=4﹣t,FT=BQ=﹣
,可求出CG,EG的长,从而可求出点E的坐标,利用待定系数法可求出直线OE的解析式,再与直线AC的解析式联立可求出点D坐标;过点B作x轴的垂线,与过点P、F作的y轴的垂线分别交于Q、T两点,先证明△PQB≌△BTF,从而有BT=PQ=4﹣t,FT=BQ=﹣![]() t2+
t2+![]() t+2,F(
t+2,F(![]() t2﹣
t2﹣![]() t+2,t﹣4),设TF交y轴于点I,根据tan∠OEG=2=tan∠OFI可得出关于t的方程,解出t可得出点P的坐标,最后根据待定系数法可求出直线PD的解析式.
t+2,t﹣4),设TF交y轴于点I,根据tan∠OEG=2=tan∠OFI可得出关于t的方程,解出t可得出点P的坐标,最后根据待定系数法可求出直线PD的解析式.
解:(1)∵直线y=kx+2经过C点,
∴C(0,2),
把点B的坐标为(4,0),C(0,2)代入y=ax2+![]() x+c,
x+c,
得到![]() ,解得
,解得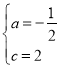 ;
;
(2)如图1,过点P作x轴的垂线,垂足为点M,且与直线AC交于点K,过点C作PK的垂线,垂足为点N,
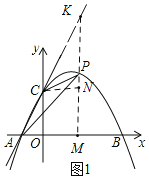
∵y=﹣![]() x2+
x2+![]() x+2,
x+2,
∴A(﹣1,0),
∵直线y=kx+2经过A点,
∴k=2,
∴y=2x+2,
∵P点的横坐标为t,
∴P(t,﹣![]() t2+
t2+![]() t+2),K(t,2t+2),
t+2),K(t,2t+2),
∴PK=![]() t2+
t2+![]() t,
t,
∴S=S△AMK﹣S△AMP﹣S△CPK=![]() ﹣
﹣![]() ﹣
﹣![]() =
=![]() =
=![]() ,
,
∴S=![]() t2+
t2+![]() t(0<t<4);
t(0<t<4);
(3)∵OC=2,OB=4,
∴tan∠OBE=![]() ,BC=2
,BC=2![]() ,
,
如图2:过点O作OH⊥BC于点H,
∴OH=![]() ,
,
∴BH=![]() =
=![]() ,
,
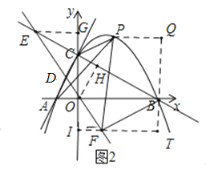
∵OE=![]() ,∴EH=
,∴EH=![]() =
=![]() ,
,
∴BE=![]() ,∴CE=
,∴CE=![]() ,
,
过点E作EG⊥y轴于点G,
∵tan∠CEG=tan∠OBE=![]() ,
,
∴CG=![]() ,EG=
,EG=![]() ,
,
∴E(﹣![]() ,
,![]() ),
),
∴易得直线OE的解析式y=﹣2x,
∵直线AC的解析式为y=2x+2,
∴联立直线OE与直线AC的解析式,解得D(﹣![]() ,1),
,1),
过点B作x轴的垂线,与过点P、F作的y轴的垂线分别交于Q、T两点,
∵∠FBP=90°,
∴∠PBQ=∠BFT,
∵BP=BF,
∴△PQB≌△BTF(AAS),
∴BT=PQ=4﹣t,FT=BQ=﹣![]() t2+
t2+![]() t+2,
t+2,
∴F(![]() t2﹣
t2﹣![]() t+2,t﹣4),
t+2,t﹣4),
设TF交y轴于点I,
∵tan∠OEG=2=tan∠OFI,
∴t﹣4=﹣2(![]() t2﹣
t2﹣![]() t+2),解得t=2或t=0(舍),
t+2),解得t=2或t=0(舍),
∴P(2,3),
设直线PD的解析式为y=kx+b,则
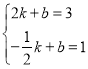 ,解得
,解得![]() ,
,
∴直线PD的解析式为y=![]() x+
x+![]() .
.