题目内容
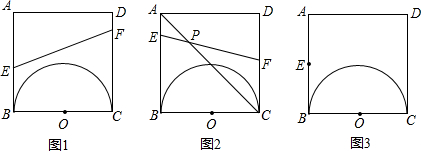
如图1,正方形ABCD中,有一直径为BC=2cm 的半圆O.两点E、F分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动.设点E离开点的B时间为t(s),其中1≤t<2.
(1)当t为何值时,线段EF和BC平行?
(2)EF能否与半圆O相切?如果能,求出t的值;如果不能,请说明原因.
(3)如图2,设EF与AC相交于点P,当点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,也请说明理由,并求AP:PC的值.
变式:如图3,若将上题改为,正方形ABCD中,有一直径为BC=2cm的半圆O.点E为AB边上的动点(不与点A、B重合),过点E与圆O相切的直线交CD所在直线为点F,设EB=x,FD=y.
(1)试写出y关于x的函数关系式,并写出自变量x的取值范围.
(2)是否存在切线EF,把正方形ABCD的周长分成相等的两部分?若存在,求出x的值.若不存在,请说明理由.
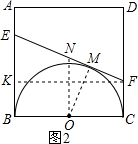
 解:(1)如图1,设E、F出发后运动了t s时,有EF和BC平行.
解:(1)如图1,设E、F出发后运动了t s时,有EF和BC平行.则BE=t,DF=2t-2.
∴t=4-2t.
解得t=
 .
.∴当t=
 s时,线段EF和BC平行.
s时,线段EF和BC平行.(2)设E、F出发后运动了t秒时,EF与半圆相切.
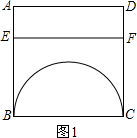
作OM⊥EF于点M,ON∥CF交EF于点N,KF∥BC交AB于点K,如图2.则
OM=1,BE=t,CF=4-2t,EK=t-(4-2t)=3t-4,ON=
 [t+(4-2t)]=2-
[t+(4-2t)]=2- t.
t.在Rt△OMN中,MN2=ON2-OM2=4t2-8t+3.
∵△OMN∽△FKE,∴
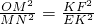 ,
,将有关数据代入上式并整理,得2t2-4t+1=0
解得t=
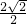 .
.∵1<t<2,∴t=
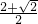 .
.∴当t=
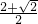 s时,线段EF与半圆相切.
s时,线段EF与半圆相切.(3)当1≤t<2时,点P的位置不会发生变化.
证明:设1≤t<2时,E、F出发后运动了t秒时,EF位置如图
则BE=t,AE=2-t,CF=4-2t
∴
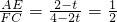
又∵AB∥DC∴△AEP∽△CFP
∴
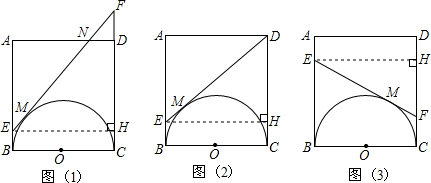
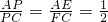 ,即点P的位置与t的取值无关.
,即点P的位置与t的取值无关.∴当1≤t<2时,点P的位置不会发生变化,且AP:PC的值为
 .
.变式题答案:
(1)如图(1),当F点在CD的延长线上,过E作EH⊥DC,交DC于F点,易证EB=EM=x,MF=FC=FD+DC=y+2,
在Rt△EHF中,由勾股定理得EH2+FH2=EF2,
即22+(y+2-x)2=(x+2+y)2,
整理得xy+2x-1=0,
∴
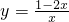
∵1-2x>0
∴
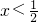
∴点F在DC上的函数关系式为
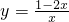 (
( )
)如图(2),当E点重合于D点时,即FD=y=0,易求出EM=EB=HC=x,DM=DC=2,
∴DH=DC-HC=2-x,
即在Rt△EHD中,ED2=EH2+HD2,
∴(x+2)2=22+(2-x)2,
解得
 ,
,如图(3),当F点在DC上,在Rt△EHF中,
由勾股定理得EH2+FH2=EF2,
即22+(y-2+x)2=(x+2-y)2,
整理得xy=2x-1,
∴
 ,
,∵2x-1>0,
∴
 ,
,∴点F在DC上的函数关系式为
 (
(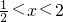 );
);(2)如图(3),假设EF把正方形周长分成相等两部分,即EA+AD+DF=EB+BC+CF,
∴2-x+2+y=x+2+2-y整理得x=y
由上面可知,
 =x,解得x=1,
=x,解得x=1,∴存在切线EF,把正方形的周长分成相等的两部分,此时x=1.
分析:(1)线段EF和BC平行时,AE=DF,2-t=2t-2,解方程就可以求出其t值.
(2)当EF与半圆O相切时,根据切线的性质,作辅助线如图,利用勾股定理和相似三角形的性质就可以求出其t的值.
(3)当1≤t<2时,△AEP∽△CFP,就可以求出点P的位置不会发生变化AP:PC=AE:CF,而AE:CF是个定值为
 .
.变式(1),当F点在CD的延长线上在Rt△EHF中;当E点重合于D点时,在Rt△EHD中;当F点在DC上,在Rt△EHF中;运用切线的性质及勾股定理建立等量关系就可以求出y关于x的函数关系式.
(2)假设EF把正方形周长分成相等两部分,即EA+AD+DF=EB+BC+CF,从而得出2-x+2+y=x+2+2-y,可以求出x与y的关系,代入图3的解析式就可以求出其值.
点评:本题考查了相似三角形的判定与性质,正方形的性质,直线与圆的位置的关系,圆的切线的性质,勾股定理的运用.

练习册系列答案
相关题目
 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上) (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )