题目内容
【题目】在同一直角坐标系中，直线y=﹣x+3与y=3x﹣5相交于C点，分别与x轴交于A、B两点．P、Q分别为直线y=﹣x+3与y=3x﹣5上的点．
（1）求△ABC的面积；
（2）若P、Q关于原点成中心对称，求P点的坐标；
（3）若△QPC≌△ABC，求Q点的坐标．
【答案】
（1）
解：依照题意画出图形，如图1所示．
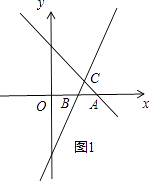
令y=﹣x+3中y=0，则x=3，
∴A（3，0）；
令y=3x﹣5中y=0，则x= 
，
∴B（ ，0）；
联立两直线解析式成方程组，得： 
，解得： 
，
∴C（2，1）．
S△ABC= 
AByC= （3﹣ ）×1= 
（2）
解：∵点P在直线y=﹣x+3上，
∴设P（m，﹣m+3），
∵P、Q关于原点成中心对称，
∴Q（﹣m，m﹣3）．
∵点Q在直线y=3x﹣5上，
∴m﹣3=﹣3m﹣5，
解得：m=﹣ ，
∴点P的坐标为（﹣ ， 
）
（3）
解：依照题意画出图形，如图2所示．
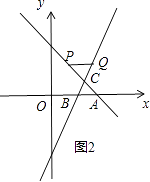
若要△QPC≌△ABC，只需PQ∥AB，且PQ=AB即可．
设P（3﹣n，n），则Q（ 
，n），
∵PQ=AB，
∴ ﹣（3﹣n）=3﹣ ，
解得：n=2，
∴点Q（ 
，2）．
【解析】（1）分别令y=﹣x+3与y=3x﹣5中y=0求出x值，即可得出点A、B的坐标，联立两直线解析式成方程组，解方程组即可求出点C的坐标，再结合三角形的面积公式即可求出△ABC的面积；（2）由点P在直线y=﹣x+3上，设点P（m，﹣m+3），由P、Q关于原点对称，由此可找出Q（﹣m，m﹣3），由点Q的坐标利用一次函数图象上点的坐标特征即可找出关于m的一元一次方程，解方程求出m值，将其代入点P的坐标中即可得出结论；（3）由△QPC≌△ABC可得出PQ∥AB，且PQ=AB，设P（3﹣n，n），则Q（ ，n），再由PQ=AB即可得出关于n的一元一次方程，解方程即可求出n值，将其代入点Q的坐标中，即可得出结论．
