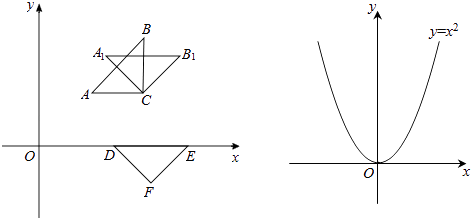
��Ŀ����
����Ŀ��������εĶ��壬���Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
��1����֪����ͼ1���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C����A=70�㣬��B=80�㣮���C����D�Ķ�����
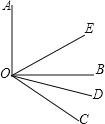
��2����̽�����ȶԽ��ı��Ρ�����ʱ��
��С�컭��һ�����ȶԽ��ı��Ρ�ABCD����ͼ2�������С�ABC=��ADC��AB=AD����ʱ������CB=CD����������֤���˽��ۣ�
���ɴ�С����룺���������⡮�ȶԽ��ı��Ρ�����һ���ڱ����ʱ����һ���ڱ�Ҳ��ȡ�������Ϊ���IJ�����ȷ������ȷ����֤����������ȷ����ٳ�������
��3����֪���ڡ��ȶԽ��ı��Ρ�ABCD�У���DAB=60�㣬��ABC=90�㣬AB=5��AD=4����Խ���AC�ij���
���𰸡�
��1��
�⣺��ͼ1
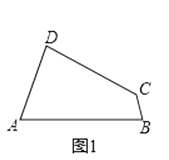
�ߵȶԽ��ı���ABCD����A�١�C��
���D=��B=80�㣬
���C=360�㩁70�㩁80�㩁80��=130�㣻
��2��
�⣺����ͼ2��
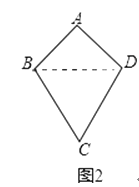
����BD��
��AB=AD��
���ABD=��ADB��
�ߡ�ABC=��ADC��
���ABC����ABD=��ADC����ADB��
���CBD=��CDB��
��CB=CD��
�ڲ���ȷ��
��������ͼ3����A=��C=90�㣬AB=AD��
��CB��CD��
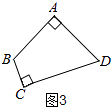
��3��
�⣺������ͼ4������ADC=��ABC=90��ʱ���ӳ�AD��BC�ཻ�ڵ�E��
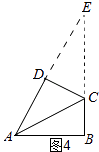
�ߡ�ABC=90�㣬��DAB=60�㣬AB=5��
��AE=10��
��DE=AE��AD=10��4=6��
�ߡ�EDC=90�㣬��E=30�㣬
��CD=2 ![]() ��
��
��AC= ![]() =
= ![]() =2
=2 ![]()
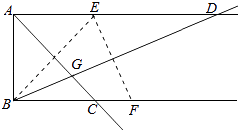
������ͼ5������BCD=��DAB=60��ʱ������D��DE��AB�ڵ�E��DF��BC�ڵ�F��
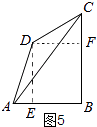
��DE��AB����DAB=60��AD=4��
��AE=2��DE=2 ![]() ��
��
��BE=AB��AE=5��2=3��
���ı���BFDE�Ǿ��Σ�
��DF=BE=3��BF=DE=2 ![]() ��
��
�ߡ�BCD=60�㣬
��CF= ![]() ��
��
��BC=CF+BF= ![]() +2
+2 ![]() =3
=3 ![]() ��
��
��AC= ![]() =
= ![]() =2
=2 ![]()
����������1�����á��ȶԽ��ı��Ρ�������������㣮��2�������õȱ߶ԵȽǺ͵ȽǶԵȱ���֤�����ھ�����ͼ����3��������ADC=��ABC=90��ʱ���ӳ�AD��BC�ཻ�ڵ�E�����ù��ɶ�����⣻������BCD=��DAB=60��ʱ������D��DE��AB�ڵ�E��DF��BC�ڵ�F������߶����ù��ɶ�����⣮