题目内容
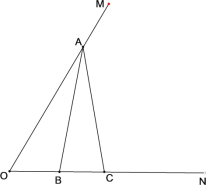
【题目】已知:如图所示,CD∥AN.
(1)用尺规作图作出∠MAN的平分线,交CD于点P.(保留作图痕迹)
(2)在(1)的基础上,若∠PAN=15°,AC=2,求点P到AM的距离.

【答案】(1)作图见解析;(2)点P到AM的距离为1.
【解析】
(1)用尺规作图作出∠MAN的平分线,交CD于点P即可;
(2) 过点P作PE⊥AM于点E,根据平行线的性质和角平分线的定义即可求出∠CAP=∠CPA,∠ECP的度数,根据等角对等边可证CA=CP,最后利用30°所对的直角边是斜边的一半即可求点P到AM的距离.
解:(1)以A为圆心,任意长度为半径作弧,交AM、AN于两点,分别以这两点为圆心,以大于![]() 这两点之间的距离为半径,作弧,两弧交于一点Q,连接AQ并延长,交CD于P,如图1所示:
这两点之间的距离为半径,作弧,两弧交于一点Q,连接AQ并延长,交CD于P,如图1所示:

射线AP即为所求作的图形;
(2)如图2,过点P作PE⊥AM于点E,

∵AP 平分∠MAN,
∴![]() ,
,
∵CD∥AN,
∴∠CPA=∠PAN,
∴∠CPA=∠MAP,
∴CP=AC=2,
∵∠PAN=15°,
∴∠MAN=2∠PAN=30°,
∵CD∥AN,
∴∠ECP=∠MAN=30°,
∵PE⊥AM,∴∠PEC=90°,
∴![]() =1,
=1,
∴点P到AM的距离为1.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目