Question

【题目】如图，∠MON60°，点A是OM边上一点，点B，C是ON边上两点，且ABAC，作点B关于OM的对称点点D，连接AD，CD，OD.

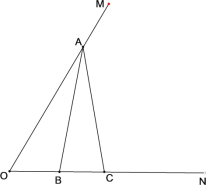
（1）依题意补全图形；

（2）猜想∠DAC °，并证明；

（3）猜想线段OA、OD、OC的数量关系，并证明.

Answer 1

【答案】（1）见解析；（2）60，证明见解析；（3）猜想：AO=OC+OD，证明见解析.

【解析】

（1）根据题意作图即可补全图形；

（2）连接BD，如图2，由点B与点D关于AO对称，可得AD＝AB，∠DAO＝∠BAO，然后利用三角形的外角性质和三角形的内角和可得∠BAC与∠OAB的关系，而∠DAC＝∠DAO+∠BAO+∠BAC，进一步即可得出∠DAC的度数；

（3）在射线CN上截取CF=BO，连接AF，如图3，先根据SAS证明△ABO≌△ACF，可得∠AFO＝∠AOB＝60°，进而可证得△AOF是等边三角形，于是AO=OF，而点B与点D关于AO对称，于是有OB=OD，进一步即可得出线段OA、OD、OC的数量关系.

解：（1）补全图形如图1：

（2）∠DAC =60°；

证明：连接BD，如图2，∵点B与点D关于AO对称，

∴BD被AO垂直平分，∴AD＝AB，∠DAO＝∠BAO，

∵AB＝AC，∴AD＝AC，

∵∠ABC＝∠ACB＝∠AOB+∠OAB=60°+∠OAB，

∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣2(60°+∠OAB)= 60°－2∠OAB，

∴∠DAC＝∠DAO+∠BAO+∠BAC＝2∠OAB+60°－2∠OAB=60°；

故答案为：60；

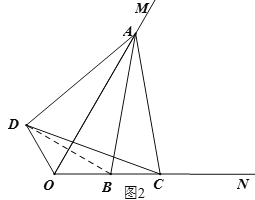
（3）猜想：AO=OC+OD.

证明：在射线CN上截取CF=BO，连接AF，如图3，

∵AB=AC，∴∠ABC＝∠ACB，∴∠ABO＝∠ACF，

∴△ABO≌△ACF（SAS），

∴∠AFO＝∠AOB＝60°，

∴△AOF是等边三角形，∴AO=OF，

∵点B与点D关于AO对称，

∴OB=OD，∴OD=CF，

∴AO=OF=OC+CF=OC+OD.