题目内容
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,已知OA=1,OC=OB.
(1)求抛物线的解析式;
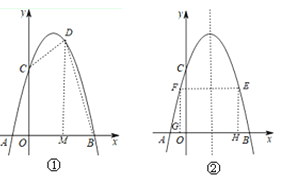
(2)若D(2,m)在该抛物线上,连接CD,DB,求四边形OCDB 的面积;
(3)设E是该抛物线上位于对称轴右侧的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点E作EH⊥x轴于点H,再过点F作FG⊥x轴于点G,得到矩形EFGH.在点E运动的过程中,当矩形EFGH为正方形时,求出该正方形的边长.
【答案】(1)y=﹣x2+3x+4.;(2)16;(3)正方形的边长为![]() 或
或![]() .
.
【解析】
(1)先求出点C的坐标,则B的坐标即可求得,利用待定系数法即可求得抛物线的解析式;
(2)求出D的坐标,作DM⊥x轴于点E.则S四边形OCDB=S梯形OCDM+S△BMD,利用C、D的坐标即可求出四边形OCDB的面积;
(3)分两种情况考虑,当点E在x轴上方和下方,根据E和F关于对称轴对称,然后利用正方形的性质即可列方程求解.
解:(1)在y=ax2+bx+4中,令x=0,得y=4,则点C的坐标是(0,4).
∵OC=OB,
∴B的坐标是(4,0).
∴抛物线的解析式为y=﹣x2+3x+4.
(2)∴点D(2,m)在抛物线y=﹣x2+3x+4上,
∴﹣4+6+4=m,解得m=6.所以D(2,6).
作DM⊥x轴于点M,如图①所示.
则S四边形OCDB=S梯形OCDM+S△BMD=![]() ×(4+6)×2+
×(4+6)×2+![]() ×2×6=10+6=16.
×2×6=10+6=16.
(3)∵抛物线的解析式为y=﹣x2+3x+4,
∴抛物线的对称轴是x=﹣![]() .
.
如图②,设点E的坐标为(x,-x2+3x+4),则点F的坐标为(3-x,-x2+3x+4),EF= x-(3-x)=2x-3.
∵四边形EFGH是正方形,
∴EF=EH.
当E在x轴上方时,2x-3=-x2+3x+4,解得x1=![]() ,x2=
,x2=![]() (舍去)
(舍去)
∴EF=![]() ;当E在x轴下方时,2x-3=-(-x2+3x+4),解得x1=
;当E在x轴下方时,2x-3=-(-x2+3x+4),解得x1=![]() ,x2=
,x2=![]() (舍去).
(舍去).
∴EF=![]() .所以正方形的边长为
.所以正方形的边长为![]() 或
或![]() .
.