题目内容
 如图,已知P、Q是△ABC的BC边上的两点,BP=PQ=QC=AP=AQ,则∠BAC的大小为
如图,已知P、Q是△ABC的BC边上的两点,BP=PQ=QC=AP=AQ,则∠BAC的大小为
- A.120°
- B.110°
- C.100°
- D.90°
A
分析:根据等边三角形的性质,得∠PAQ=∠APQ=∠AQP=60°,再根据等腰三角形的性质和三角形的外角的性质求得∠BAP=∠CAQ=30°,从而求解.
解答:∵BP=PQ=QC=AP=AQ,
∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.
又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,
∴∠BAP=∠CAQ=30°.
∴∠BAC=120°.
故选A.
点评:此题主要运用了等边三角形的性质、等腰三角形的性质以及三角形的外角的性质.
分析:根据等边三角形的性质,得∠PAQ=∠APQ=∠AQP=60°,再根据等腰三角形的性质和三角形的外角的性质求得∠BAP=∠CAQ=30°,从而求解.
解答:∵BP=PQ=QC=AP=AQ,
∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.
又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,
∴∠BAP=∠CAQ=30°.
∴∠BAC=120°.
故选A.
点评:此题主要运用了等边三角形的性质、等腰三角形的性质以及三角形的外角的性质.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 8、如图,已知△ABC的周长是34,其中AB=10,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )
8、如图,已知△ABC的周长是34,其中AB=10,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )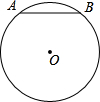 如图,已知⊙O的半径是10,弦AB长为16.现要从弦AB和劣弧
如图,已知⊙O的半径是10,弦AB长为16.现要从弦AB和劣弧
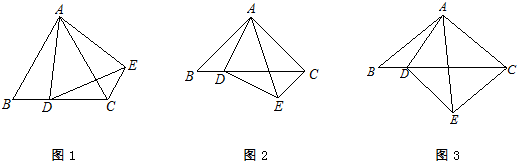
 (2010•西藏)如图,已知E,F是四边形ABCD的对角线BD上两点,BF=DE,AF=CE,AF∥CE,
(2010•西藏)如图,已知E,F是四边形ABCD的对角线BD上两点,BF=DE,AF=CE,AF∥CE, 如图,已知△ABC,P是边AB上一点,连接CP,使△ACP∽△ABC成立的条件是( )
如图,已知△ABC,P是边AB上一点,连接CP,使△ACP∽△ABC成立的条件是( )