题目内容
将进货单价为30元的商品按40元出售时,每天卖出500件。据市场调查发现,如果这种商品每件涨价1元,其每天的销售量就减少10件。
(1)要使得每天能赚取8000元的利润,且尽量减少库存,售价应该定为多少?
(2)售价定为多少时,每天获得的利润最大?最大利润为多少?
(1) .(2)当x=60时,
.(2)当x=60时,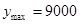 .
.
解析试题分析:(1)设售价定为x元时,每件赚取利润为(x-30)元,每天买出【500-10(x-40)】件,每天赚取利润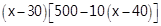 等于8000元,列方程即可. (2)设最大利润为y元,由题可得:y=
等于8000元,列方程即可. (2)设最大利润为y元,由题可得:y=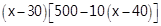

 由二次函数的性质可得结论.
由二次函数的性质可得结论.
试题解析:(1)解:设售价定为x元时,每天赚取利润8000元,
由已知得: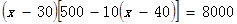
整理得: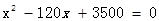
解得: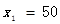 或
或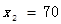
 尽量减少库存,
尽量减少库存,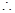

答:售价定为50元时,每天赚取利润8000元。
(2)解:设最大利润为y元,由题可得: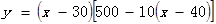 .
.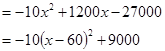
当x=60时,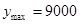 .
.
考点:1.一元二方程的应用.2.二次函数的性质.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目


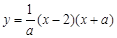
 与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
 顶点的纵坐标y与横坐标x之间的关系式.
顶点的纵坐标y与横坐标x之间的关系式. ).
).
 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: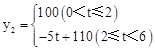

 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).