题目内容
如图,已知抛物线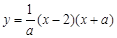
 与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线过点M(-2,-2),求实数a的值;
(2)在(1)的条件下,解答下列问题:
①求出△BCE的面积;
②在抛物线的对称轴上找一点P,使CP+EP的值最小,求出点P的坐标.
(1)a=4;(2)①6;②P(-1,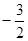 ).
).
解析试题分析:(1)将点(-2,-2)代入抛物线的解析式,即可求出a的值;(2)①令y=0,代入抛物线解析式,即可求出相应的x的值,从而求出点B、C的坐标,令x=0,代入抛物线解析式,可求出对应的y的值,从而求出点E的坐标,然后利用三角形面积公式,即可求得△BCE的面积;②由于点B、C关于抛物线的对称轴对称,所以连接BE,交对称轴于点P,此交点即为所求的位置,此时,BE的值就是PC+PE的最小值,由于点B、E的坐标已求出,所以可用待定系数法求得直线BE的解析式,从而求出点P的坐标.
试题解析:(1)∵点M(-2,-2)在抛物线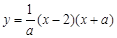 上,
上,
∴ ,
,
解得: ;
;
(2)①由(1)得抛物线解析式为 ,
,
令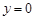 时,得:
时,得: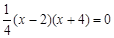 ,
,
解得: ,
,
∵点B在点C的左侧,
∴B(﹣4,0),C(2,0),
∴ ,
,
当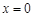 时,得:
时,得: ,
,
∴E(0,-2),
∴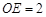 ,
,
∴ ;
;
②由抛物线解析式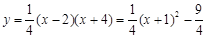 ,得对称轴为直线
,得对称轴为直线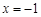 ,
,
根据C与B关于抛物线对称轴直线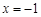 对称,连接BE,与对称轴交于点P,即为所求,
对称,连接BE,与对称轴交于点P,即为所求,
设直线BE解析式为 ,
,
将B(﹣4,0),E(0,-2)代入得: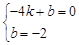 ,
,
解得: ,
,
∴直线BE解析式为 ,
,
将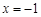 代入
代入 ,
,
得: ,
,
∴P(﹣1, ).
).
考点:1、利用轴对称求最短距离;2、二次函数的图象和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ).
).
 与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).



