题目内容
如图,已知△OAB的顶点A(﹣6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
(1)写出C,D两点的坐标;
(2)求过A,D,C三点的抛物线的解析式,并求此抛物线顶点E的坐标;
(3)证明AB⊥BE.
(1)C(2,0),D(0,6);(2)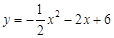 ,顶点E的坐标是(-2,8);(3)详见解析.
,顶点E的坐标是(-2,8);(3)详见解析.
解析试题分析:本题考查了旋转的性质,二次函数的解析式及顶点坐标的求法,勾股定理的逆定理,综合性较强,难度不大.运用待定系数法求二次函数的解析式是中考的常考点,需熟练掌握,解题时根据条件设出适当的解析式,能使计算简便.(1)根据旋转的性质,可得OC=OB,OD=OA,进而可得C、D两点的坐标;
(2)由于抛物线过点A(-6,0),C(2,0),所以设抛物线的解析式为y=a(x+6)(x-2)(a≠0),再将D(0,6)代入,求出a的值,得出抛物线的解析式,然后利用配方法求出顶点E的坐标;(3)已知A、B、E三点的坐标,运用两点间的距离公式计算得出AB2=40,BE2=40,AE2=80,则AB2+BE2=AE2,根据勾股定理的逆定理即可证明AB⊥BE.
试题解析:
解:(1)∵将△OAB绕点O按顺时针旋转90°,得到△ODC,
∴△ODC≌△OAB,
∴OC=OB=2,OD=OA=6,
∴C(2,0),D(0,6);
(2)∵抛物线过点A(-6,0),C(2,0),
∴可设抛物线的解析式为y=a(x+6)(x-2)(a≠0),
∵D(0,6)在抛物线上,
∴6=-12a,
解得a=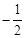 ,
,
∴抛物线的解析式为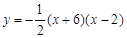
∴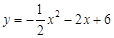
∵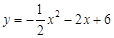
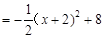
∴顶点E的坐标为(-2,8);
(3)连接AE.
∵A(-6,0),B(0,2),E(-2,8),
∴AB2=62+22=40,BE2=(-2-0)2+(8-2)2=40,AE2=(-2+6)2+(8-0)2=80,
∴AB2+BE2=AE2,
∴AB⊥BE.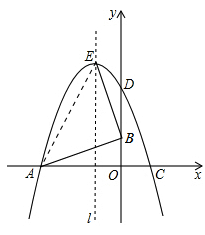
考点:1、二次函数综合题;2、旋转的性质.

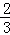 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边). 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
 ,
, ).
).
 .
.
 的解集.
的解集. (
( ).
). 轴的交点坐标;
轴的交点坐标; 的值;
的值; 的图象与抛物线始终只有一个公共点,求一次函数的解析式.
的图象与抛物线始终只有一个公共点,求一次函数的解析式. 与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).