题目内容
如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为 时,四边形PQAC是平行四边形;当点P的坐标为 时,四边形PQAC是等腰梯形. (利用备用图画图,直接写出结果,不写求解过程).
(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标
(1)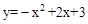 ,(1,4);(2)(2,3);(
,(1,4);(2)(2,3);( );(3)四边形PMAC的面积取得最大值为
);(3)四边形PMAC的面积取得最大值为 ,此时点P的坐标为(
,此时点P的坐标为( ).
).
解析试题分析:(1)将抛物线的解析式设为交点式,可用待定系数法较简捷地求得抛物线的解析式,将其化为顶点式即可求得顶点D的坐标.
(2)①如图1,四边形PQAC是平行四边形时,
∵CP∥x轴,点P在抛物线上,∴点P与点C关于抛物线的对称轴x=1对称.
∵C(0,3),∴P(2,3).
②如图2,四边形PQAC是等腰梯形时,设P(m, ),
),
过点P作PH⊥x轴于点H,则H(m,0).
易得△ACO∽△QNP,∴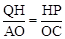 .
.
∵OA=1,OC=3,HP= ,∴
,∴ ,即
,即 .
.
∴AQ=AO+OH-QH= 。∴
。∴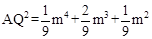 .
.
又由勾股定理得, .
.
由四边形PQAC是等腰梯形得AQ=CP,即AQ2=CP2,
∴ ,整理得
,整理得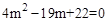 ,解得
,解得 或
或 .
.
当 时,由①知CP∥AQ,四边形PQAC是平行四边形,不符合条件,舍去.
时,由①知CP∥AQ,四边形PQAC是平行四边形,不符合条件,舍去.
当 时,CP与AQ不平行,符合条件。∴P(
时,CP与AQ不平行,符合条件。∴P( ).
).
(3)求出直线BD的解析式,设定点P的坐标,由 列式,根据二次函数最值原理,即可求得四边形PMAC的面积的最大值和此时点P的坐标.
列式,根据二次函数最值原理,即可求得四边形PMAC的面积的最大值和此时点P的坐标.
试题解析:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0),
∴可设抛物线的解析式为 .
.
又∵抛物线y=ax2+bx+c(a≠0) 与y轴交于点C(0,3),
∴ ,解得
,解得 .
.
∴抛物线的解析式为 ,即
,即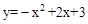 .
.
又∵ ,∴抛物线顶点D的坐标为(1,4).
,∴抛物线顶点D的坐标为(1,4).
(2)(2,3);( ).
).
(3)设直线BD的解析式为 ,
,
由B(3,0),D(1,4)得 ,解得
,解得 .
.
∴直线BD的解析式为 .
.
∵点P在直线PD上,∴设P(p, ).
).
则OA=1,OC=3,OM= p,PM= .
.
∴ .
.
∵ ,∴当
,∴当 时,四边形PMAC的面积取得最大值为
时,四边形PMAC的面积取得最大值为 ,此时点P的坐标为(
,此时点P的坐标为( ).
).
考点:1.二次函数综合题;2.待定系数法;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5.平行四边形的判定;6.等腰梯形的判定;7.相似三角形的判定和性质勾股定理;8.解一元二次方程.

 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
 (
( ).
). 轴的交点坐标;
轴的交点坐标; 的值;
的值; 的图象与抛物线始终只有一个公共点,求一次函数的解析式.
的图象与抛物线始终只有一个公共点,求一次函数的解析式. 与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
 ,抛物线
,抛物线 过A、B两点.
过A、B两点.

 的图象
的图象 ,将其向右平移两个单位后得到图象
,将其向右平移两个单位后得到图象 .
.
 轴相交于点
轴相交于点 、点
、点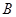 (点
(点 ,点
,点 位于
位于 轴负半轴上,且到
轴负半轴上,且到 所在直线的解析式.
所在直线的解析式.