ΧβΡΩΡΎ»ί
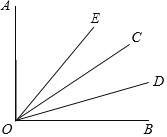
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§÷±œΏDE…œ”–“ΜΒψOΘ§ΙΐΒψO‘Ύ÷±œΏDE…œΖΫΉς…δœΏOCΘ§ΓœCOEΘΫ140ΓψΘ§ΫΪ“Μ÷±Ϋ«»ΐΫ«ΑεAOBΒΡ÷±Ϋ«ΕΞΒψΖ≈‘ΎΒψO¥ΠΘ§“ΜΧθ÷±Ϋ«±ΏOA‘Ύ…δœΏOD…œΘ§Νμ“Μ±ΏOB‘Ύ÷±œΏDE…œΖΫΘ§ΫΪ÷±Ϋ«»ΐΫ«Αε»ΤΉ≈ΒψOΑ¥ΟΩΟκ10ΓψΒΡΥΌΕ»Ρφ ±’κ–ΐΉΣ“Μ÷ήΘ§…η–ΐΉΣ ±ΦδΈΣtΟκΘ°
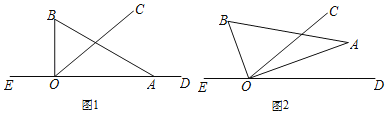
Θ®1Θ©Β±÷±Ϋ«»ΐΫ«Αε–ΐΉΣΒΫ»γΆΦ2ΒΡΈΜ÷Ο ±Θ§OA«ΓΚΟΤΫΖ÷ΓœCODΘ§«σ¥Υ ±ΓœBOCΒΡΕ» ΐΘΜ
Θ®2Θ©»τ…δœΏOCΒΡΈΜ÷Ο±Θ≥÷≤Μ±δΘ§‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥Ηω ±ΩΧΘ§ ΙΒΟ…δœΏOAΓΔOCΓΔOD÷–ΒΡΡ≥“ΜΧθ…δœΏ «ΝμΝΫΧθ…δœΏΥυ≥…Φ–Ϋ«ΒΡΫ«ΤΫΖ÷œΏΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωtΒΡ»Γ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τ‘Ύ»ΐΫ«ΑεΩΣ ΦΉΣΕ·ΒΡΆ§ ±Θ§…δœΏOC“≤»ΤOΒψ“‘ΟΩΟκ15ΓψΒΡΥΌΕ»Ρφ ±’κ–ΐΉΣ“Μ÷ήΘ§¥”–ΐΉΣΩΣ ΦΕύ≥Λ ±ΦδΘ§…δœΏOCΤΫΖ÷ΓœBODΘ°÷±Ϋ”–¥≥ωtΒΡ÷ΒΘ°Θ®±ΨΧβ÷–ΒΡΫ«ΨυΈΣ¥σ”Ύ0Γψ«“–Γ”Ύ180ΓψΒΡΫ«Θ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΓœBOCΘΫ70ΓψΘΜΘ®2Θ©¥φ‘ΎΘ§tΘΫ2Θ§tΘΫ8Μρ32ΘΜΘ®3Θ©![]() Μρ
Μρ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΆΦΩ…÷ΣΓœBOCΘΫΓœAOB©¹ΓœAOCΘ§ΓœAOCΩ…άϊ”ΟΫ«ΤΫΖ÷œΏΦΑΤΫΫ«ΒΡΕ®“ε«σ≥ω.
Θ®2Θ©Ζ÷OAΤΫΖ÷ΓœCODΘ§OCΤΫΖ÷ΓœAODΘ§ODΤΫΖ÷ΓœAOC»ΐ÷÷«ιΩωΖ÷±πΫχ––Χ÷¬έΘ§Ϋ®ΝΔΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω….
Θ®3Θ©Ζ÷±π”ΟΚ§tΒΡ¥ζ ΐ Ϋ±μ Ψ≥ωΓœCODΚΆΓœBODΘ§‘ΌΗυΨίOCΤΫΖ÷ΓœBODΫ®ΝΔΖΫ≥ΧΫβΖΫ≥ΧΦ¥Ω…Θ§ΉΔ“βΖ÷«ιΩωΧ÷¬έ.
Θ®1Θ©ΫβΘΚΓΏΓœCOEΘΫ140ΓψΘ§
ΓύΓœCODΘΫ180Γψ©¹ΓœCOEΘΫ40ΓψΘ§
”÷ΓΏOAΤΫΖ÷ΓœCODΘ§
ΓύΓœAOCΘΫ![]() ΓœCODΘΫ20ΓψΘ§
ΓœCODΘΫ20ΓψΘ§
ΓΏΓœAOBΘΫ90ΓψΘ§
ΓύΓœBOCΘΫ90Γψ©¹ΓœAOCΘΫ70ΓψΘΜ
Θ®2Θ©¥φ‘Ύ
ΔΌΒ±OAΤΫΖ÷ΓœCOD ±Θ§ΓœAODΘΫΓœAOCΘ§Φ¥10ΓψtΘΫ20ΓψΘ§ΫβΒΟΘΚtΘΫ2ΘΜ
ΔΎΒ±OCΤΫΖ÷ΓœAOD ±Θ§ΓœAOCΘΫΓœDOCΘ§Φ¥10Γψt©¹40ΓψΘΫ40ΓψΘ§ΫβΒΟΘΚtΘΫ8ΘΜ
ΔέΒ±ODΤΫΖ÷ΓœAOC ±Θ§ΓœAODΘΫΓœCODΘ§Φ¥360Γψ©¹10ΓψtΘΫ40ΓψΘ§ΫβΒΟΘΚtΘΫ32ΘΜ
Ήέ…œΥυ ωΘΚtΘΫ2Θ§tΘΫ8Μρ32ΘΜ
Θ®3Θ©![]() Μρ
Μρ![]() Θ§άμ”…»γœ¬ΘΚ
Θ§άμ”…»γœ¬ΘΚ
…η‘ΥΕ· ±ΦδΈΣtΘ§‘ρ”–
ΔΌΒ±90+10tΘΫ2Θ®40+15tΘ© ±Θ§tΘΫ![]()

ΔΎΒ±270©¹10tΘΫ2Θ®320©¹15tΘ© ±Θ§tΘΫ![]()

Υυ“‘tΒΡ÷ΒΈΣ![]() Μρ
Μρ![]() Θ°
Θ°

 Κ°ΦΌΧλΒΊ÷Ί«λ≥ωΑφ…γœΒΝ–¥πΑΗ
Κ°ΦΌΧλΒΊ÷Ί«λ≥ωΑφ…γœΒΝ–¥πΑΗ