题目内容
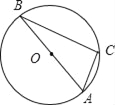
【题目】如图,⊙O是△ABC外接圆,直径AB=12,∠A=2∠B.
(1)∠A= °,∠B= °;
(2)求BC的长(结果用根号表示);
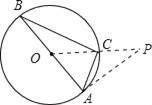
(3)连接OC并延长到点P,使CP=OC,连接PA,画出图形,求证:PA是⊙O的切线.
【答案】(1)∠A=60°,∠B=30°;(2)6![]() ;(3)见解析
;(3)见解析
【解析】分析:(1)、不难看出∠C应该是直角,∠A=2∠B,那么这两个角的度数就容易求得了;(2)、直角三角形ABC中,有斜边AB的长,有三角的度数,BC的值就能求出了;(3)、此题实际上是证明PA⊥AB,由图我们不难得出△AOC是等边三角形,那么就容易证得△ABC≌△OPA,这样就能求出PA⊥AB了.
详解:(1)∵∠C=90°,∠A=2∠B, ∴∠A=60°,∠B=30°;
(2)∵AB为直径, ∴∠ACB=90°, 又∵∠B=30°, ∴AC=![]() AB=65.
AB=65.
∴BC=![]() =6
=6![]() ;
;
(3)如图,∵OP=2OC=AB, ∵∠BAC=60°,OA=OC, ∴△OAC为等边三角形.
∴∠AOC=60°. 在△ABC和△OPA中,∵AB=OP,∠BAC=∠POA=60°,AC=OA,
∴△ABC≌△OPA. ∴∠OAP=∠ACB=90°. ∴PA是⊙O的切线.

练习册系列答案
相关题目