题目内容
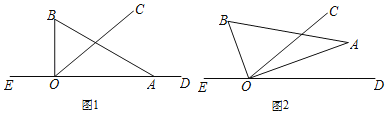
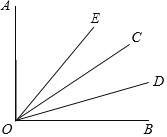
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠AOE=2∠COE.若∠DOE=36°,求∠EOC的度数.
【答案】18°
【解析】
根据互余的定义可得∠AOB=90°,由角平分线和角的和与差可得:∠AOE=54°﹣∠BOD,∠COE=36°﹣∠BOD,根据∠AOE=2∠COE,列等式可得结论.
解:∵∠AOC与∠BOC互余,
∴∠AOB=∠AOC+∠BOC=90°.
∵OD平分∠BOC,
∴∠BOD=∠COD,
∵∠DOE=36°,
∴∠AOE=∠AOB﹣∠DOE﹣∠BOD
=90°﹣36°﹣∠BOD
=54°﹣∠BOD,
∠COE=∠DOE﹣∠COD=36°﹣∠BOD,
∵∠AOE=2∠COE,
∴54°﹣∠BOD=2(36°﹣∠BOD),
解得:∠BOD=18°,
∴∠EOC=36°﹣∠BOD=36°﹣18°=18°.

练习册系列答案
相关题目