题目内容
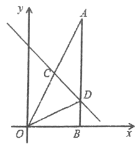
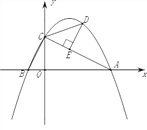
【题目】已知直线y=-![]() x+2与x轴、y轴分别交于点A、C,抛物线y=-
x+2与x轴、y轴分别交于点A、C,抛物线y=-![]() x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作
x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作![]() 于点E.
于点E.
(1)求抛物线的表达式;
(2)求△ACD面积的最大值;
(3)若△CED与△COB相似,求点D的坐标.
【答案】(1)![]() ;(2)4;(3)点D的坐标为D1(3,2)、D2(
;(2)4;(3)点D的坐标为D1(3,2)、D2(![]() ,
,![]() ).
).
【解析】分析:(1)根据直线y=-![]() x+2与x轴,y轴相交于点A,C,求点A,C的坐标,用待定系数法求抛物线的解析式;(2)过点D作DG⊥x轴于点G,交AC于点F,设D(t,
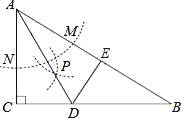
x+2与x轴,y轴相交于点A,C,求点A,C的坐标,用待定系数法求抛物线的解析式;(2)过点D作DG⊥x轴于点G,交AC于点F,设D(t,![]() ),由S△ACD=S△CDF+S△ADF,用含t的代数式表示S△ACD,结合二次函数的性质求解;(3)除了∠BOC=∠CED外,△BOC与△CDE的对应关系不确定,所以需要分两类讨论,①当∠DCE=∠BCO时,可得CD∥AB,点C,D的纵坐标相等;②当∠DCE=∠CBO时,将△OCA沿AC翻折得△MCA,点O的对称点为点M,过点M作MH⊥y轴于点H,AN⊥MH于点N,利用相似三角形的性质和勾股定理求出点M的坐标后,再由直线CM与抛物线的交点列方程组求解.
),由S△ACD=S△CDF+S△ADF,用含t的代数式表示S△ACD,结合二次函数的性质求解;(3)除了∠BOC=∠CED外,△BOC与△CDE的对应关系不确定,所以需要分两类讨论,①当∠DCE=∠BCO时,可得CD∥AB,点C,D的纵坐标相等;②当∠DCE=∠CBO时,将△OCA沿AC翻折得△MCA,点O的对称点为点M,过点M作MH⊥y轴于点H,AN⊥MH于点N,利用相似三角形的性质和勾股定理求出点M的坐标后,再由直线CM与抛物线的交点列方程组求解.
详解:(1)∵直线![]() 与x轴.y轴分别交于点A.C,
与x轴.y轴分别交于点A.C,
∴A(4,0),C(0,2),OA=4,OC=2,
将A(4,0),C(0,2)分别代入![]() 中,
中,
![]() ,解得
,解得![]() .
.
∴![]() .
.
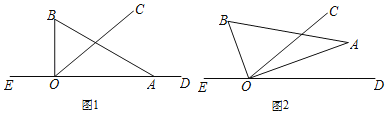
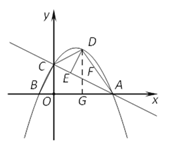
(2)如图1,过点D作DG⊥x轴于点G,交AC于点F,
设D(t,![]() ),其中
),其中![]() ,则F(t,
,则F(t,![]() ).
).
∴DF=![]() -(
-(![]() )=
)=![]() ,
,
S△ACD=S△CDF+S△ADF
=![]()
=![]()
=![]()
=![]()
=![]() .
.
∴当t=2时,S△ACD最大=4.
(3)设y=0,则![]() =0,解得
=0,解得![]() ,
,![]() ,
,
∴B(-1,0),OB=1.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵∠BOC=∠COA=90°,
∴△BOC∽△COA,
∴∠OCB=∠OAC,∴∠OCA=∠OBC.
①当∠DCE=∠BCO时,∠DCE=∠OAC,
∴CD∥OA,点D的纵坐标与点C纵坐标相等,
令y=2,则![]() =2,解得
=2,解得![]() ,
,![]() ,
,
∴D1(3,2).
②如图2,当∠DCE=∠CBO时,∠DCE=∠OCA,
将△OCA沿AC翻折得△MCA,点O的对称点为点M,
过点M作MH⊥y轴于点H,AN⊥MH于点N,
则CM=CO=2,AM=AO=4,
设HM=m,MN=HN-HM=OA-HM=4-m,
由∠AMC=∠AOC=∠ANM=∠MHC=90°易证△CHM∽△MNA,且相似比![]() ,
,
∴AN=2MH=2m,CH=![]() MN=2-
MN=2-![]() m,
m,
在Rt△CMH中,由勾股定理得:![]() ,解得
,解得![]() ,
,![]() ,
,
∴MH=![]() ,OH=
,OH=![]() ,M(
,M(![]() ,
,![]() ).
).
设直线CM的表达式为y=kx+n,则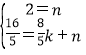 ,解得
,解得![]() ,
,
∴![]() ,
,
由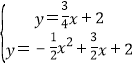 ,解得
,解得![]() ,
,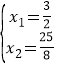 ,
,
∴D2(![]() ,
,![]() ).
).
综上所述,点D的坐标为D1(3,2).D2(![]() ,
,![]() ).
).


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案