题目内容
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 . 
【答案】![]() ≤a≤3﹣
≤a≤3﹣ ![]()
【解析】解:①当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,
正方形边长a的值最小,AC是正方形的对角线,
∴AC=A′D= ![]() ,
,
∴a= ![]() ,
,
②当正方形ABCD的四个顶点都在正六边形的边上时,正方形边长a的值最大,AC是正方形的对角线AC,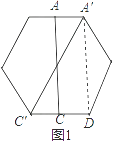
设A′(t, ![]() )时,正方形的边长最大,
)时,正方形的边长最大,
∵OB′⊥OA′,
∴B′(﹣ ![]() ,t),
,t),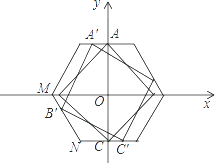
设直线MN的解析式为y=kx+b,M(﹣1,0),N(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴ 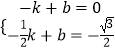 ,
,
∴ ![]() ,
,
∴直线MN的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
将B′(﹣ ![]() ,t)代入得t=
,t)代入得t= ![]() ﹣
﹣ ![]() ,
,
此时,A′B′取最大值,
∴a= ![]() =3﹣
=3﹣ ![]() ,
,
∴正方形边长a的取值范围是: ![]() ≤a≤3﹣
≤a≤3﹣ ![]() ,
,
故答案为: ![]() ≤a≤3﹣
≤a≤3﹣ ![]() .
.
①当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,正方形边长a的值最小,AC是正方形的对角线,先利用锐角三角函数的定义求出AC的长,再根据勾股定理求出正方形的边长a;②当正方形ABCD的四个顶点都在正六边形的边上时,正方形边长a的值最大,AC是正方形的对角线AC,设点设A′(t, ![]() )时,正方形的边长最大,根据OB′⊥OA′,表示出点B′(﹣
)时,正方形的边长最大,根据OB′⊥OA′,表示出点B′(﹣![]() ,t),从而可得出点M、N的坐标,求出直线MN的函数解析式,再将点B′的坐标代入直线MN的函数解析式,求出t的值,然后利用勾股定理求出a的值,即可得到a的取值范围。
,t),从而可得出点M、N的坐标,求出直线MN的函数解析式,再将点B′的坐标代入直线MN的函数解析式,求出t的值,然后利用勾股定理求出a的值,即可得到a的取值范围。

练习册系列答案
相关题目