题目内容
【题目】如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= . 
【答案】72°
【解析】解:连接OA、OB、OC,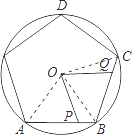
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,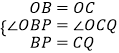 ,
,
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
连接OA、OB、OC,根据正五边形的性质得出∠AOB=∠BOCOA=OB,OB=OC,可证明∠OBA=∠OCB,再证明△OBP≌△OCQ,得出∠BOP=∠COQ,再证明∠POQ=∠BOC,即可得出答案。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目