题目内容
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.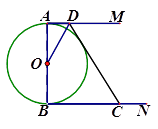
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.
【答案】
(1)证明:过O做OE⊥CD于点E,
则∠OED=90°
∵⊙O与AM相切于点A
∴∠OAD=90°
∵OD平分∠ADE
∴∠ADO=∠EDO
∵OD=OD
∴△OAD≌△OED
∴OE=OA
∵OA是⊙O的半径
∴OE是⊙O的半径
∴CD是⊙O的切线
(2)解:过点D做DF⊥BC于点F,则DF=AB=x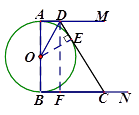
∵AD=4,BC=y
∴CF=BC-AD=y-4
由切线长定理可得:
∴DE=DA,CE=CB
∴CD=CE+ED
=BC+AD
=4+y
在Rt△DFC中,
∵CD2=DF2+FC2
∴(y+4)=x 2+(y-4)2
整理得:y= ![]() x2
x2
则y关于x的函数关系式为:y= ![]() x2
x2
解法二:连接OC,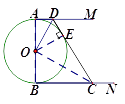
∵CD、CB都是⊙O的切线
∴CE=CB=y
OC平分∠BCD
即:∠OCD= ![]() ∠BCD
∠BCD
同理:DE=AD=4
∠CDO= ![]() ∠CDA
∠CDA
∵AM、BN分别与⊙O相切
且AB为⊙O的直径
∴AM//BN
∴∠BCD+∠CDA=180°
∴∠OCD+∠CDO=90°
∵∠CDO+∠OCD+∠COD=180°
∴∠COD=90°
∵在Rt△DOC中,
OD2=OA2+AD2
即OD2=( ![]() )2+42
)2+42
同理可得:
OC2=( ![]() )2+y2
)2+y2
∵CD=CE+ED=y+4
∴在Rt△OCD中
CD2=OC2+OD2
即(y+4)2=( ![]() )2+42+(
)2+42+( ![]() )2+y2
)2+y2
整理得:y= ![]() x2
x2
则y关于x的函数关系式为:y= ![]() x2
x2
【解析】(1)过O做OE⊥CD于点E,则∠OED=90° ,根据切线的性质,圆的切线垂直于经过切点的半径得出∠OAD=90° ,根据角平分线的定义得出∠ADO=∠EDO ,从而根据AAS判断出△OAD≌△OED,根据全等三角形的对应边相等得出OE=OA ,根据切线的判定定理得出CD是⊙O的切线 ;
(2)解法一 :过点D做DF⊥BC于点F,则DF=AB=x ,根据矩形的性质及线段的和差得出CF=BC-AD=y-4 ,由切线长定理可得:DE=DA,CE=CB ,根据线段的和差得出CD=CE+ED=BC+AD=4+y ,在Rt△DFC中,由勾股定理得出(y+4)=x 2+(y-4)2 ,从而得出y与x之间的函数关系式 ;解法二:连接OC,根据切线长定理得出CE=CB=y ,OC平分∠BCD ,即:∠OCD= ![]() ∠BCD,同理:DE=AD=4 ,∠CDO=
∠BCD,同理:DE=AD=4 ,∠CDO= ![]() ∠CDA ,又AM、BN分别与⊙O相切且AB为⊙O的直径 ,故AM//BN,根据二直线平行同旁内角互补得出∠BCD+∠CDA=180° ,进而得出∠OCD+∠CDO=90° ,根据平角的定义得出∠CDO+∠OCD+∠COD=180° ,从而得出COD=90°,在Rt△DOA中,根据勾股定理得出OD2=(
∠CDA ,又AM、BN分别与⊙O相切且AB为⊙O的直径 ,故AM//BN,根据二直线平行同旁内角互补得出∠BCD+∠CDA=180° ,进而得出∠OCD+∠CDO=90° ,根据平角的定义得出∠CDO+∠OCD+∠COD=180° ,从而得出COD=90°,在Rt△DOA中,根据勾股定理得出OD2=( ![]() )2+42 , 同理可得:OC2=( x 2 )2+y2 ,由于CD=CE+ED=y+4 ,在Rt△OCD中 ,CD2=OC2+OD2 ,即(y+4)2=( x 2 )2+42+( x 2 )2+y2 ,从而得出y与x之间的函数关系。
)2+42 , 同理可得:OC2=( x 2 )2+y2 ,由于CD=CE+ED=y+4 ,在Rt△OCD中 ,CD2=OC2+OD2 ,即(y+4)2=( x 2 )2+42+( x 2 )2+y2 ,从而得出y与x之间的函数关系。
【考点精析】本题主要考查了切线长定理和垂径定理的推论的相关知识点,需要掌握从圆外一点引圆的两条切线,它们的切线长相等圆心和这一点的连线平分两条切线的夹角;推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等才能正确解答此题.