题目内容
【题目】如图,正五边形ABCDE中.
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
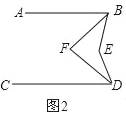
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
【答案】
(1)证明:如图1中,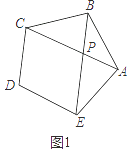
∵五边形ABCDE是正五边形,
∴∠BCD=∠BAE=108°,
∵AB=AE,
∴∠ABE=∠AEB=36°,
∴∠CBE=72°,
∴∠DCB+∠CBE=180°,
∴CD∥BE,
同法可证,AC∥DE,
∴∴四边形PEDC是平行四边形,
∵CD=DE,
∴四边形PEDC是菱形
(2)证明:如图2中,连接AN.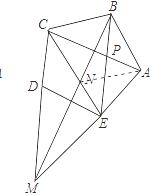
∵∠MCA=∠MAC=72°,
∴MC=MA,
∵BC=BA,
∴BM垂直平分线段AC,
∴NC=NA,
∴∠NCA=∠NAC=∠CEP=36°,
∵∠PAE=∠NEA=72°,
∴∠PEA=∠NAE=36°,
∵AE=EA,
∴△PAE≌△NEA,
∴AN=PE,
∴CN=PE
(3)![]() +1
+1
【解析】(3)解:如图3中.在AD上取一点W,使得AW=WE.设AW=x.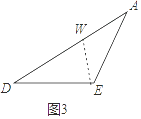
∵∠A=∠D=∠AEW=36°,
∴∠DWE=∠DEW=72°,
∴DW=DE=2,
∵∠A=∠A,∠AEW=∠D,
∴△AWE∽△AED,
∴AE2=AWAD,
∴22=x(x+2),
解得x= ![]() ﹣1,
﹣1,
∴AD=2+x= ![]() +1,
+1,
故答案为 ![]() +1
+1
(1)根据正五边形的性质及等腰三角形的性质求出∠DCB和∠CBE的度数,就可证明∠DCB+∠CBE=180°,可得CD∥BE,同法可证AC∥ED,由此根据菱形的判定即可证明。
(2)如图2中,连接AN,先根据MC=MA,BC=BA得出BM垂直平分线段AC,得出CN=AN,再证明△PAE≌△NEA,即可解决问题。
(3)如图3中.在AD上取一点W,使得AW=WE.设AW=x,相聚已知条件证明△AWE∽△AED,可得AE2=AWAD,构建方程即可解决问题。