Question

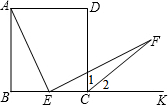
已知：如图，在正方形ABCD中，F是AD的中点，BF与AC交于点G，则△BFC与四边形CGFD的面积之比是______．

Answer 1

∵F是AD的中点，
∴AF=

1

2

AD=

1

2

BC，
设正方形的边长是a，则△BFC的面积是

1

2

a²，△ABC的面积是

1

2

a²，
AF=

a

2

，S_△ABF=

1

2

×

a

2

×a=

a2

4

，

FG

BG

=

1

2

，
∴S_△AFG=

1

3

S_△AFB=

a2

12

，
∴四边形CGFD的面积a²-

1

2

a²-

a2

12

=

5a2

12

，
∴△BFC与四边形CGFD的面积之比是6：5．
故答案为：6：5．